题目内容
求证:一元二次方程ax2+bx+c=0(a≠0)最多有两个不相等的根.
证明：假设方程有三个互不相等的根x1、x2、x3,
则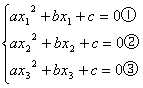
由①-②,得a(x1+x2)+b=0,④
由①-③,得a(x1+x3)+b=0,⑤
由④-⑤,得a(x2-x3)=0.
∵a≠0,∴x2-x3=0,即x2=x3,这与假设x1≠x2≠x3矛盾.
∴原方程最多只有两个不相等的根.
练习册系列答案
金钥匙试卷系列答案
相关题目
金钥匙试卷系列答案题目内容
求证:一元二次方程ax2+bx+c=0(a≠0)最多有两个不相等的根.
证明：假设方程有三个互不相等的根x1、x2、x3,
则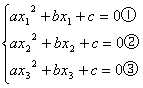
由①-②,得a(x1+x2)+b=0,④
由①-③,得a(x1+x3)+b=0,⑤
由④-⑤,得a(x2-x3)=0.
∵a≠0,∴x2-x3=0,即x2=x3,这与假设x1≠x2≠x3矛盾.
∴原方程最多只有两个不相等的根.
金钥匙试卷系列答案