题目内容
在△ABC中,已知a2=b2+c2+bc,则角A等于 .
【答案】分析:利用余弦定理表示出cosA,把已知的等式变形后代入求出cosA的值,由A为三角形的内角,利用特殊角的三角函数值即可求出A的度数.
解答:解:∵a2=b2+c2+bc,
∴b2+c2-a2=-bc,
根据余弦定理得:cosA=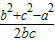 =-
=- ,
,
又A∈(0,180°),
则角A=120°.
故答案为:120°
点评:此题考查了余弦定理,以及特殊角的三角函数值,熟练掌握余弦定理的结构特征是解本题的关键,同时注意角度的范围.
解答:解:∵a2=b2+c2+bc,
∴b2+c2-a2=-bc,
根据余弦定理得:cosA=
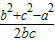 =-
=- ,
,又A∈(0,180°),
则角A=120°.
故答案为:120°
点评:此题考查了余弦定理,以及特殊角的三角函数值,熟练掌握余弦定理的结构特征是解本题的关键,同时注意角度的范围.

练习册系列答案
相关题目