题目内容
正方形ABCD在平面M的同一侧,若A、B、C三点到M的距离分别是2、3、4,则直线BD与平面M的位置关系是
BD∥平面M
BD∥平面M
.分析:因为AB∥CD,AB=CD,并且B比A高1,所以C比D高1,可得点D到平面的距离为3,再利用空间中点与平面的位置关系可得答案.
解答:解:因为AB∥CD,AB=CD,并且B比A高1,
所以C比D高1,
所以点D到平面的距离为3,
因为正方形ABCD在平面M的同一侧,并且B点到M的距离是3,
所以直线BD∥平面M.
故答案为:BD∥平面M
所以C比D高1,
所以点D到平面的距离为3,
因为正方形ABCD在平面M的同一侧,并且B点到M的距离是3,
所以直线BD∥平面M.
故答案为:BD∥平面M
点评:本题主要考查空间中点、线、面的位置关系,考查学生的空间想象能力,此题属于基础题.

练习册系列答案
相关题目

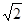 ,则AC与平面α所成角的大小是
,则AC与平面α所成角的大小是