题目内容

边长为2的正方形ABCD在平面α内的射影是EFCD，如果AB与平面α的距离为
2
，则AC与平面α所成角的大小是
 
．
分析：AB与平面α的距离为
2
，那么AC=2
2
，可求AC与平面α所成角的大小．
解答：解：AB与平面α的距离为
2
，则A到平面的距离是
2
，边长为2的正方形ABCD，那么AC=2
2
，则AC与平面α所成角为θ
则sinθ=
1
2
，∴θ=30°
故答案为：30°．
点评：本题考查空间直线与平面之间的位置关系，斜线与平面所成的角，是基础题．
练习册系列答案
相关题目
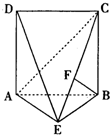精英家教网如图，直二面角D-AB-E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE．
（Ⅰ）求证AE⊥平面BCE；
（Ⅱ）求二面角B-AC-E的大小；
（Ⅲ）求点D到平面ACE的距离．
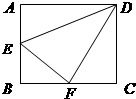如图，边长为2的正方形ABCD中，
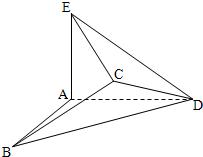（1）E、F是AB、BC的中点，将△AED、△DCF分别沿DE、DF折起，使AC两点重合于点A′，求证：A′D⊥EF；
（2）若BE=BF=λBC，求λ的范围并求三棱锥A′-EFD的体积．
若将边长为2的正方形ABCD沿对角线BD折成一个直二面角，且EA⊥平面ABD，AE=a（如图）．
（Ⅰ）若a=2
2
，求证：AB∥平面CDE；
（Ⅱ）求实数a的值，使得二面角A-EC-D的大小为60°．
（2013•昌平区二模）如图，在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，侧面PAD⊥底面ABCD，且PA=PD=
2
2
AD，E、F分别为PC、BD的中点．
（Ⅰ） 求证：EF∥平面PAD；
（Ⅱ） 求证：面PAB⊥平面PDC；
（Ⅲ） 在线段AB上是否存在点G，使得二面角C-PD-G的余弦值为
1
3
？说明理由．
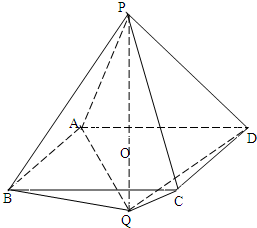如图：长为3的线段PQ与边长为2的正方形ABCD垂直相交于其中心O（PO＞OQ）．
（1）若二面角P-AB-Q的正切值为-3，试确定O在线段PQ的位置；
（2）在（1）的前提下，以P，A，B，C，D，Q为顶点的几何体PABCDQ是否存在内切球？若存在，试确定其内切球心的具体位置；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网