题目内容
如图,在底面是正方形的四棱锥P―ABCD中,PA=AC=2,PB=PD=![]()

(1)证明PA⊥平面ABCD;
(2)已知点E在PD上,且PE:ED=2:1,点F为棱PC的中点,证明BF//平面AEC。
(3)求四面体FACD的体积.
证明:(I)因为在正方形ABCD中,AC=2
∴AB=AD=![]()
可得:在△PAB中,PA2+AB2=PB2=6。
所以PA⊥AB
同理可证PA⊥AD
故PA⊥平面ABCD
(II)取PE中点M,连接FM,BM,连接BD交AC于O,连接OE
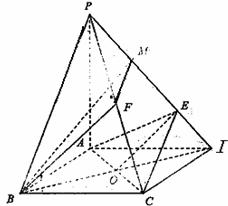
∵F,M分别是PC,PF的中点,
∴FM∥CE,
又FM![]() 面AEC,CE
面AEC,CE![]() 面AEC
面AEC
∴FM∥面AEC
又E是DM的中点
OE∥BM,OE![]() 面AEC,BM
面AEC,BM![]() 面AEC
面AEC
∴BM∥面AEC且BM∩FM=M
∴平面BFM∥平面ACE
又BF![]() 平面BFM,∴BF∥平面ACE
平面BFM,∴BF∥平面ACE
(3)连接FO,则FO∥PA,因为PA⊥平面ABCD,则FO⊥平面ABCD,所以FO=1,
SACD=1,
∴VFACD=VF――ACD=![]()

练习册系列答案
相关题目
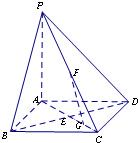 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.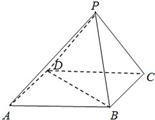 如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2. 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点. 如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.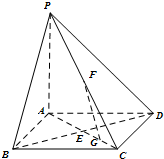 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.