Question

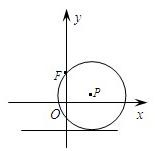
已知圆P过点F(0，

1

4

)，且与直线y=-

1

4

相切．
（Ⅰ）求圆心P的轨迹M的方程；
（Ⅱ）若直角三角形ABC的三个顶点在轨迹M上，且点B的横坐标为1，过点A、C分别作轨迹M的切线，两切线相交于点D，直线AC与y轴交于点E，当直线BC的斜率在[3，4]上变化时，直线DE斜率是否存在最大值，若存在，求其最大值和直线BC的方程；若不存在，请说明理由？

Answer 1

（Ⅰ）依题意圆心P到点F的距离与到定直线y=-

1

4

的距离相等，
根据抛物线的定义可知P的轨迹为抛物线，
设方程为x²=2py，p=

1

2

，所以x²=y
（Ⅱ）B（1，1），设A（x₁，x₁²），C（x₂，x₂²），kAC=

x12-x22

x1-x2

=x1+x2
设BC的斜率为k，则

y-1=k(x-1) x2=y

?x2-kx+k-1=0，△=k²-4k+4≥0，
又1+x_c=k，?x_c=k-1，C（k-1，（k-1）²），A(-

1

k

-1，(

1

k

+1)2)，kAC=x1+x2=k-

1

k

-2，
直线AC的方程为y-(k-1)2=(k-

1

k

-2)[x-(k-1)]，
令x=0，y=k-

1

k

，所以E(0，k-

1

k

)
AD：y-x₁²=2x₁（x-x₁）?y=2x₁x-x₁²
同理CD：y=2x₂x-x₂²，联立两方程得D(

1

2

(k-

1

k

-2)，

1

k

-k)kED=

k- 1 k +k- 1 k

1 2 (2+ 1 k -k)

=

2(k- 1 k )

1 2 (2+ 1 k -k)

=-4

k2-1

-k2+2k+1

=-4(1+

2

2+ 1 k -k

)
令u=

1

k

-k，则u在[3，4]上递减，所以，当k=3时，k_ED最大为8
所以，BC的方程为y-1=3（x-1），即3x-y-2=0