题目内容
研究双曲线方程：9y2-16x2=144，下列判断正确 的是
- A.实轴长是8
- B.离心率为
- C.渐近线方程为
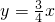
- D.焦点在x轴
A
分析：向将双曲线转化为标准形式，得到a，b，c的值，即可得到实轴长、焦点坐标、离心率和渐近线方程．
解答：由9y2-16x2=144得：
-
=1，
∴a=4，b=3，c=5．
实轴长8，焦点坐标F1（0，-5），F2（0，5），离心率e=
，渐近线方程为y=±
x．
故选A．
点评：本题考查双曲线的标准方程，以及双曲线的简单性质的应用，令标准方程中的“1”为“0”即可求出渐近线方程．
分析：向将双曲线转化为标准形式，得到a，b，c的值，即可得到实轴长、焦点坐标、离心率和渐近线方程．
解答：由9y2-16x2=144得：
-=1，∴a=4，b=3，c=5．
实轴长8，焦点坐标F1（0，-5），F2（0，5），离心率e=
，渐近线方程为y=±x．故选A．
点评：本题考查双曲线的标准方程，以及双曲线的简单性质的应用，令标准方程中的“1”为“0”即可求出渐近线方程．
练习册系列答案
相关题目
