题目内容
已知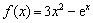 ,函数
,函数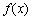 的零点从小到大依次为
的零点从小到大依次为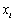 ,
,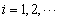 .
.
(Ⅰ)若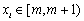 (
(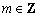 ),试写出所有的
),试写出所有的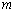 值;
值;
(Ⅱ)若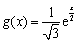 ,
,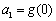 ,
,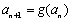 ,求证:
,求证: 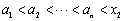 ;
;
(Ⅲ)若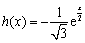 ,
,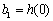 ,
,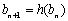 ,试把数列
,试把数列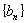 的前
的前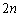 项及
项及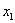 按从小到大的顺序排列。(只要求写出结果).
按从小到大的顺序排列。(只要求写出结果).
解:(Ⅰ)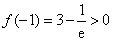 ,
,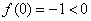 ,
,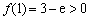 ,
,
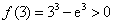 ,
,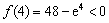
所以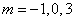 …………3分
…………3分
(Ⅱ)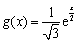 ,
,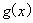 在
在 上单调递增,当
上单调递增,当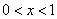 时,
时,
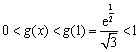 , …………1分
, …………1分
由(Ⅰ)知,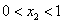 ,
,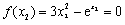 ,
,
即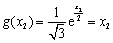 …………2分
…………2分
所以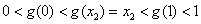 ①
①
下面用数学归纳法证明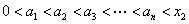
由式①知,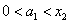 ,所以
,所以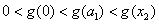 ,
,
即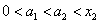 ,所以,当
,所以,当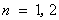 时,命题成立
时,命题成立
假设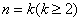 时命题成立,即
时命题成立,即
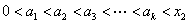 ②
②
当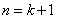 时,由式②得
时,由式②得
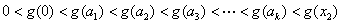
即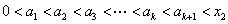
当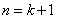 时,命题也成立,
时,命题也成立,
所以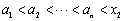 …7分
…7分
(Ⅲ)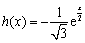 ,
,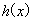 在R上单调递减,由于
在R上单调递减,由于 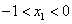 ,所以
,所以
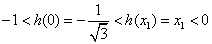 ,即
,即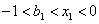 ,可推出
,可推出
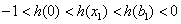 ,即
,即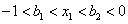
进而可得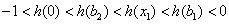 ,
,
即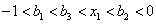 ,又可得
,又可得
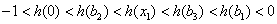
即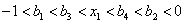 ,所以用数学归纳法易证
,所以用数学归纳法易证
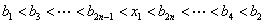

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
某网站体育版块足球栏目组发起了“射手的上一场进球与本场进球有无关系”的调查活动,在所有参与调查的人中,持“有关系”“无关系”“不知道”态度的人数如表所示:
| 有关系 | 无关系 | 不知道 | |
| 人数 | 500 | 600 | 900 |
(1)在所有参与调查的人中,用分层抽样的方法抽取样本,已知从持“有关系”态度的人中抽取了5人,求总样本容量。
(2)持“有关系”态度的人中,40岁以下和40岁以上(含40岁)的比例为2:3,从抽取的5个样本中,再任选2人作访问,求至少1人在40岁以下的概率;
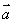 与
与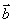 的夹角为
的夹角为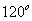 ,
, ,
, ,则
,则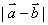 = .
= .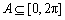 ,集合
,集合 ,若
,若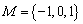 ,则不同集合A的个数是
,则不同集合A的个数是 .
.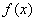 的最小正周期及单调减区间;
的最小正周期及单调减区间; ,
,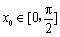 ,求
,求 的值.
的值. 成立的实数a的范围是 .
成立的实数a的范围是 .  满足
满足 当-1≤x<3时,
当-1≤x<3时, A.2013 B.2012 C.338 D.337
A.2013 B.2012 C.338 D.337 ,则
,则 ( )
( )  ,
, B.
B. 


 D.
D.