题目内容
7.已知函数f(x)=sin2$\frac{ωx}{2}$+$\frac{1}{2}$sinωx-$\frac{1}{2}$(ω>0),x∈R,若f(x)在区间(π,2π)内有零点,则ω的取值范围是( )| A. | ($\frac{1}{4}$,$\frac{5}{8}$)∪($\frac{5}{4}$,+∞) | B. | (0,$\frac{1}{4}$]∪[$\frac{5}{8}$,1) | C. | ($\frac{1}{8}$,$\frac{1}{4}$)∪($\frac{5}{8}$,$\frac{5}{4}$) | D. | ($\frac{1}{8}$,$\frac{1}{4}$)∪($\frac{5}{8}$,+∞) |
分析 利用两角和与差的三角函数化简函数的解析式,利用零点求出x的值,然后利用特殊值排除选项推出结果即可.
解答 解:f(x)=$\frac{1-cosωx}{2}+\frac{sinωx}{2}$$-\frac{1}{2}$=$\frac{\sqrt{2}}{2}$sin (ωx-$\frac{π}{4}$),由f(x)=0,可得 x=$\frac{(4k+1)π}{4ω}$(k∈Z),
令ω=2得函数f(x)有一零点x=$\frac{9π}{8}$∈(π,2π),排除(B)、(C),
令$ω=\frac{3}{8}$得函数f(x)在(0,+∞)上的零点从小到大为:x1=$\frac{2π}{3}$,x2$\frac{10π}{3}$,…
显然x1∉(π,2π),x2∉(π,2π),可排除(A),
故选:D.
点评 本题考查函数的零点的判断与应用,三角函数的化简求值,考查转化思想.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
17.已知命题p:?x∈R,x2+ax+a2≥0(a∈R),命题q:$?{x_0}∈{N^*}$,$2x_0^2-1≤0$,则下列命题中为真命题的是( )
| A. | p∧q | B. | p∨q | C. | (?p)∨q | D. | (?p)∧(?q) |
2.己知0<a<b<l<c,则( )
| A. | ab>aa | B. | ca>cb | C. | logac>logbc | D. | logbc>logb a |
12.已知集合$A=\{x|{log_{\frac{1}{3}}}(4-x)>-1\}$,B={x|4x-1>8},若全集为实数集R,则A∩(∁RB)=( )
| A. | $(-∞,\frac{5}{2}]$ | B. | (2,4) | C. | $(\frac{5}{2},4)$ | D. | (1,$\frac{5}{2}$] |
19.已知O为直角坐标系的坐标原点,双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(b>a>0)$上有一点$P(\sqrt{5},m)$(m>0),点P在x轴上的射影恰好是双曲线C的右焦点,过点P作双曲线C两条渐近线的平行线,与两条渐近线的交点分别为A,B,若平行四边形PAOB的面积为1,则双曲线的标准方程是( )
| A. | ${x^2}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{2}-\frac{y^2}{3}=1$ | C. | ${x^2}-\frac{y^2}{6}=1$ | D. | $\frac{x^2}{{\frac{3}{2}}}-\frac{y^2}{{\frac{7}{2}}}=1$ |
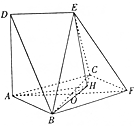 如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF,且∠DAF=90°.
如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF,且∠DAF=90°.