题目内容
已知f(x)=ln(x2+1),g(x)=(
)x-m,若?x1∈[0,3],?x2∈[1,2],使得f(x1)≥g(x2),则实数m的取值范围是( )
| 1 |
| 2 |
A.[
| B.(-∞,
| C.[
| D.(-∞,-
|
要使命题成立需满足f(x1)min≥g(x2)min,
函数f(x)=ln(x2+1)在[0,3]上是增函数,所以f(x1)min=f(0)=0,
函数g(x)=(
)x-m在[1,2]上是减函数,所以g(x2)min=g(2)=(
)2-m,
∴0≥(
)2-m,
∴m≥
.
故选A.
函数f(x)=ln(x2+1)在[0,3]上是增函数,所以f(x1)min=f(0)=0,
函数g(x)=(
| 1 |
| 2 |
| 1 |
| 2 |
∴0≥(
| 1 |
| 2 |
∴m≥
| 1 |
| 4 |
故选A.

练习册系列答案
相关题目
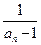 = bn,
= bn,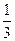 }是等比数列 ⑵判断{an}是否为无穷数列。
}是等比数列 ⑵判断{an}是否为无穷数列。 +
+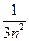 )<
)<