题目内容
16．解不等式|x-3|＜|2x-1|分析 要解的不等式等价于 （x-3）2＜（2x-1）2，即 3x2+2x-8＞0，由此求得x的范围．
解答 解：不等式|x-3|＜|2x-1|，等价于（x-3）2＜（2x-1）2，即 3x2+2x-8＞0，
即 x＜-2，或＞$\frac{4}{3}$，故原不等式的解集为{x|x＜-2，或＞$\frac{4}{3}$ }．
点评 本题主要考查绝对值不等式的解法，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
7．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{3}，0≤x＜1}\\{f（x-1），x≥1}\end{array}\right.$，若g（x）=f（x）-kx-2k有5个不同的零点，则实数k的取值范围是（ ）
| A． | [$\frac{1}{7}$，$\frac{1}{6}$] | B． | [$\frac{1}{7}$，$\frac{1}{6}$） | C． | [$\frac{1}{8}$，$\frac{1}{7}$） | D． | （$\frac{1}{8}$，$\frac{1}{7}$] |
1．设函数f（x）=|lgx|，则关于x的方程f2（x）+mf（x）+n=0恰有三个不同实数解的充要条件是（ ）
| A． | m＜0且n＜0 | B． | m＞0且n＜0 | C． | m＜0且n=0 | D． | m＞0且n=0 |
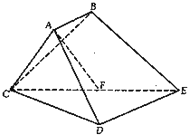已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，AC=AD=CD=DE=2，AB=1，F为CE的中点．