题目内容
（2012•江门一模）（几何证明选讲选做题）如图，E、F是梯形ABCD的腰AD、BC上的点，其中CD=2AB，EF∥AB，若
| EF |
| AB |
| CD |
| EF |
| AE |
| ED |
| ||
| 2 |
| ||
| 2 |
分析：说明梯形AEFD、EBCF相似，EF与AB的关系，根据相似多边形的对应边比例关系，因而可以把求
转化为求
．
| AE |
| ED |
| AB |
| EF |
解答：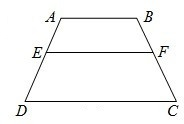
解：因为
=
，EF∥AB，所以梯形AEFD∽梯形EBCF，
∴EF2=AB•CD=2AB2，EF=
AB，
并且
=
=
=
．
故答案为：
．
解：因为| EF |
| AB |
| CD |
| EF |
∴EF2=AB•CD=2AB2，EF=
| 2 |
并且
| AE |
| ED |
| AB |
| EF |
| AB | ||
|
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题考查了相似多边形的对应边的比相等．
练习册系列答案
相关题目
（2012•江门一模）如图，某几何体的正视图和侧视图都是对角线长分别为4和3的菱形，俯视图是对角线长为3的正方形，则该几何体的体积为（ ）
（2012•江门一模）如图，四边形ABCD中，AB=5，AD=3，cosA=