题目内容
 如图在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,
如图在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD, ,求面SCD与面SEA所成二面角的正切值.
,求面SCD与面SEA所成二面角的正切值.
 解:建立如图所示的空间直角坐标系,则A(0,0,0,),B(-1,0,0),C(-1,1,0),
解:建立如图所示的空间直角坐标系,则A(0,0,0,),B(-1,0,0),C(-1,1,0), ,S(0,0,1),
,S(0,0,1),延长CD交x轴于点F,则F(1,0,0),
作AE⊥SF于点E,连接DE,则
由于SA=AF且SA⊥AF,得
 ,
,∴
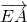 =
= ,
,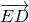 =
=
∴
 ,
,∴

∴
 ,
,故面SCD与面SBA所成二面角的正切值为
 .
.分析:建立空间直角坐标系,延长CD交x轴于点F,作AE⊥SF于点E,连接DE,利用向量的夹角公式,即可求得结论、
点评:本题考查面面角,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
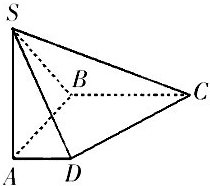 如图在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,
如图在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,
 ,BC=6.
,BC=6.
 ,BC=6.
,BC=6.