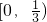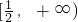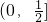题目内容
若在区间(-1,1)内任取实数a,在区间(0,1)内任取实数b,则直线ax-by=0与圆(x-1)2+(y-2)2=1相交的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:由题意可得本题是几何概率模型,先求构成试验的全部区域:
所围成的图形的面积,记:“直线ax-by=0与圆(x-1)2+(y-2)2=1相交”为事件A,则由直线与圆相交的性质可得,
<1整理可得4a-3b>0,再求构成区域A的面积,代入几何概型计算公式可求
|
| |a-2b| | ||
|
解答:解:由题意可得构成试验的全部区域为:
所围成的边长分别为1,2的矩形,面积为2
记:“直线ax-by=0与圆(x-1)2+(y-2)2=1相交”为事件A
则由直线与圆相交的性质可得,
<1整理可得4a-3b>0,构成区域A为图中阴影部分,面积为(
+1)×1×
=
由几何概率的计算公式可得,P(A)=
=
故选B.

|
记:“直线ax-by=0与圆(x-1)2+(y-2)2=1相交”为事件A
则由直线与圆相交的性质可得,
| |a-2b| | ||
|
| 1 |
| 4 |
| 1 |
| 2 |
| 5 |
| 8 |
由几何概率的计算公式可得,P(A)=
| ||
| 2 |
| 5 |
| 16 |
故选B.

点评:本题主要考查了与面积有关的几何概率的求解,解题的关键是要能求出构成试验的全部区域的图象的面积及基本事件的图象的面积,还利用了点到直线的距离公式解决直线与圆的位置关系.

练习册系列答案
相关题目
函数f(x)为偶函数,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上,g(x)=f(x)-mx-m有两个零点,则实数m的取值范围是( )
A、[0,
| ||
B、[
| ||
C、[0,
| ||
D、(0,
|
若函数f(x)=3ax+1-2a在区间(-1,1)上存在一个零点,则a的取值范围是( )
A、a>
| ||
B、a>
| ||
C、-1<a<
| ||
| D、a<-1 |
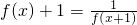 ,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上,g(x)=f(x)-mx-m有两个零点,则实数m的取值范围是
,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上,g(x)=f(x)-mx-m有两个零点,则实数m的取值范围是