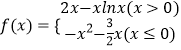Question

【题目】如甲图所示，在矩形ABCD中，AB=4，AD=2，E是CD的中点，将△ADE沿AE折起到△D1AE位置，使平面D1AE⊥平面ABCE，得到乙图所示的四棱锥D1﹣ABCE．
（Ⅰ）求证：BE⊥平面D1AE；
（Ⅱ）求二面角A﹣D1E﹣C的余弦值．

Answer 1

【答案】证明：（Ⅰ）如图，取AE中点F，连D1F， 在△AD1E中，∵D1A=D1E=2，∴D1F⊥AE，
又∵平面D1AE⊥平面ABCE，∴D1F⊥平面ABCE，
∵BE平面ABCE，∴D1F⊥BE．
在△ABE中，可得 ，BE=2 ，AB=4，
∴BE⊥AE，又∵D1F∩AE=F，
∴BE⊥平面D1AE；
（Ⅱ）解：由题意，取AB中点G，以E为坐标原点，分别以EG，EC为x，y轴正方向建立空间直角坐标系E﹣xyz．

如图所示，则E（0，0，0），C（0，2，0）D1（1，﹣1， ），B（2，2，0），
由（Ⅰ）知： 是平面AD1E的法向量，
设平面CED1的法向量为 ，则
，令z=1，则x=﹣ ，y=0，
∴ ，
设二面角A﹣D1E﹣C的平面角为θ，
则|cosθ|=|cos＜ ＞|=| |= ．
由图可知，二面角A﹣D1E﹣C的平面角为钝角，
∴cos ，
即二面角A﹣D1E﹣C的余弦值为 ．
【解析】（Ⅰ）取AE中点F，连D1F，求解三角形可得D1F⊥AE，又平面D1AE⊥平面ABCE，利用面面垂直的性质可得D1F⊥平面ABCE，从而得到D1F⊥BE．在△ABE中，可得BE⊥AE，再利用线面垂直的判定可得BE⊥平面D1AE；（Ⅱ）由题意，取AB中点G，以E为坐标原点，分别以EG，EC为x，y轴正方向建立空间直角坐标系E﹣xyz．求出所用点的坐标，得到平面AD1E与平面CED1的法向量．利用两法向量所成角的余弦值可得二面角A﹣D1E﹣C的余弦值．
【考点精析】通过灵活运用直线与平面垂直的判定，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想即可以解答此题．