题目内容
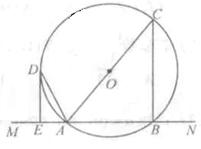
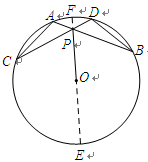
如图,直线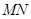 交圆
交圆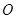 于
于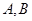 两点,
两点,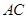 是直径,
是直径,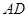 平分
平分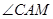 ,交圆
,交圆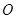 于点
于点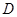 , 过
, 过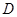 作
作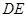 丄
丄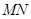 于
于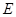 .
.
(1)求证: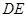 是圆
是圆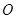 的切线;
的切线;
(2)若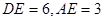 ,求
,求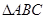 的面积
的面积
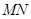 交圆
交圆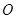 于
于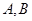 两点,
两点,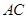 是直径,
是直径,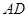 平分
平分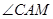 ,交圆
,交圆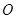 于点
于点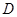 , 过
, 过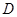 作
作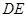 丄
丄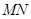 于
于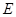 .
.
(1)求证:
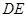 是圆
是圆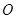 的切线;
的切线;(2)若
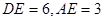 ,求
,求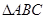 的面积
的面积(1)连结OD,则OA=OD,所以∠OAD=∠ODA.,然后利用∠EDA+∠ODA=90°,即DE⊥OD来得到证明。
(2)54.
(2)54.
试题分析:(Ⅰ)连结OD,则OA=OD,所以∠OAD=∠ODA.
因为∠EAD=∠OAD,所以∠ODA=∠EAD.
因为∠EAD+∠EDA=90°,所以∠EDA+∠ODA=90°,即DE⊥OD.
所以DE是圆O的切线.


(Ⅱ)因为DE是圆O的切线,所以DE2=EA·EB,
即62=3(3+AB),所以AB=9.
因为OD∥MN, 所以O到MN的距离等于D到MN的距离,即为6
又因为O为AC的中点,C到MN的距离等于12
故△ABC的面积S=
 AB·BC=54.
AB·BC=54.点评:主要是考查了圆的切线定义以及切割线定理的运用,属于基础题。

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
 =
= ,
, =3,则AE∶EC=________.
=3,则AE∶EC=________.
 切⊙
切⊙ 于点
于点 ,割线
,割线 经过圆心
经过圆心 于点
于点 ,
, ,
, ,则
,则 _______.
_______.
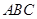 中,
中,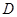 是边
是边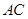 的中点,点
的中点,点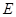 在线段
在线段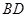 上,且满足
上,且满足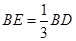 ,延长
,延长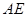 交
交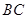 于点
于点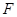 ,则
,则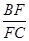 的值为 .
的值为 . 的半径为3,两条弦
的半径为3,两条弦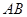 ,
,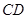 交于点
交于点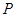 ,且
,且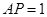 ,
, 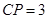 ,
,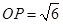 .
.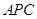 ≌△
≌△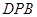 .
.
 是圆
是圆 的直径,点
的直径,点 在圆
在圆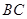 到
到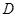 使
使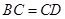 ,过
,过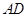 于
于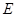 .若
.若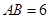 ,
,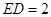 ,则
,则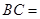 _________.
_________.
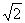 ,
,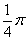 ),曲线C的参数方程为
),曲线C的参数方程为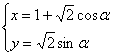 (
(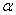 为参数),则点M到曲线C上的点的距离的最小值为 .
为参数),则点M到曲线C上的点的距离的最小值为 .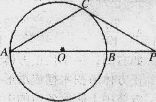
 圆周,C点是弧BE上的任意一点, △ABD是等边三角形,则四边形ABCD的周长p的取值范围是
圆周,C点是弧BE上的任意一点, △ABD是等边三角形,则四边形ABCD的周长p的取值范围是 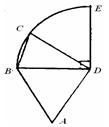
 是半圆
是半圆 的直径,
的直径, 是半圆
是半圆 的点,
的点, ,垂足为
,垂足为 . 若
. 若 ,
, ,则
,则 .
.