题目内容
选修4-5:不等式选讲 设函数f(x)=|x+1|+|x-4|-a.
(1)当a=1时,求函数f(x)的最小值;
(2)若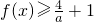 对任意的实数x恒成立,求实数a的取值范围.
对任意的实数x恒成立,求实数a的取值范围.
解:(1)当a=1时,f(x)=|x+1|+|x-4|-1≥|(x+1)-(x-4)|-1=5-1=4.
所以函数f(x)的最小值为4.
(2)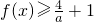 对任意的实数x恒成立?|x+1|+|x-4|-1≥a+
对任意的实数x恒成立?|x+1|+|x-4|-1≥a+ 对任意的实数x恒成立?a+
对任意的实数x恒成立?a+ ≤4对任意实数x恒成立.
≤4对任意实数x恒成立.
当a<0时,上式显然成立;
当a>0时,a+ ≥2
≥2 =4,当且仅当a=
=4,当且仅当a= 即a=2时上式取等号,此时a+
即a=2时上式取等号,此时a+ ≤4成立.
≤4成立.
综上,实数a的取值范围为(-∞,0)∪{2}.
分析:(1)当a=1时,利用绝对值不等式的性质即可求得最小值;
(2)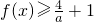 ?|x+1|+|x-4|-1≥a+
?|x+1|+|x-4|-1≥a+ ?a+
?a+ ≤4,对a进行分类讨论可求a的取值范围.
≤4,对a进行分类讨论可求a的取值范围.
点评:本题考查绝对值函数、基本不等式以及恒成立问题,考查分类讨论思想,恒成立问题一般转化为函数最值问题解决,.
所以函数f(x)的最小值为4.
(2)
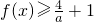 对任意的实数x恒成立?|x+1|+|x-4|-1≥a+
对任意的实数x恒成立?|x+1|+|x-4|-1≥a+ 对任意的实数x恒成立?a+
对任意的实数x恒成立?a+ ≤4对任意实数x恒成立.
≤4对任意实数x恒成立.当a<0时,上式显然成立;
当a>0时,a+
 ≥2
≥2 =4,当且仅当a=
=4,当且仅当a= 即a=2时上式取等号,此时a+
即a=2时上式取等号,此时a+ ≤4成立.
≤4成立.综上,实数a的取值范围为(-∞,0)∪{2}.
分析:(1)当a=1时,利用绝对值不等式的性质即可求得最小值;
(2)
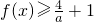 ?|x+1|+|x-4|-1≥a+
?|x+1|+|x-4|-1≥a+ ?a+
?a+ ≤4,对a进行分类讨论可求a的取值范围.
≤4,对a进行分类讨论可求a的取值范围.点评:本题考查绝对值函数、基本不等式以及恒成立问题,考查分类讨论思想,恒成立问题一般转化为函数最值问题解决,.

练习册系列答案
相关题目