题目内容
在三棱柱 中,各棱长相等,侧棱垂直于底面,点
中,各棱长相等,侧棱垂直于底面,点 是侧面
是侧面 的中心,则
的中心,则 与平面
与平面 所成角的大小是 ( )
所成角的大小是 ( )
A.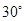 | B. | C. | D. |
C
解析试题分析:
如图,取BC中点E,连接DE、AE、AD,
依题意知三棱柱为正三棱柱,
易得AE⊥平面 ,故∠ADE为AD与平面
,故∠ADE为AD与平面 所成的角.
所成的角.
设各棱长为1,则AE= ,
,
DE=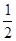 ,tan∠ADE=
,tan∠ADE=  =
=  ,
,
∴∠ADE=60°.
考点:空间中直线与平面之间的位置关系.
点评:求直线和平面所成的角时,应注意的问题是:(1)先判断直线和平面的位置关系.(2)当直线和平面斜交时,常用以下步骤:①构造--作出或找到斜线与射影所成的角;②设定--论证所作或找到的角为所求的角;③计算--常用解三角形的方法求角;④结论--点明斜线和平面所成的角的值.

练习册系列答案
相关题目
设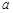 、
、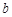 是不同的两条直线,
是不同的两条直线,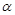 、
、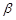 是不同的两个平面,分析下列命题,其中正确的是( ).
是不同的两个平面,分析下列命题,其中正确的是( ).
A.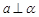 , ,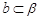 , ,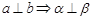 | B.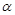 ∥ ∥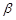 , ,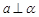 , ,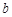 ∥ ∥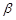 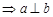 |
C.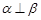 , ,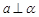 , ,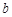 ∥ ∥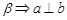 | D.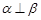 , ,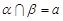 , , |
如图,在正方体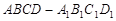 中,
中,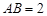 .则点
.则点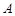 到面
到面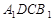 的距离是( )
的距离是( )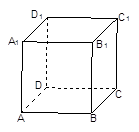
A.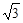 | B.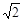 | C.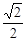 | D.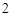 |
已知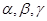 是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①
是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①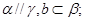 ②
②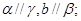 ③
③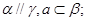 如果命题
如果命题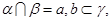 且_______,则
且_______,则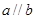 为真命题,则可以在横线处填入的条件是( )
为真命题,则可以在横线处填入的条件是( )
| A.①或② | B.②或③ | C.①或③ | D.只有② |
a,b,c表示三条不重合的直线,M表示平面,给出下列四个命题:①若a∥M,b∥M,则a∥b;②若b M,a∥b,则a∥M;③若a⊥c,b⊥c,则a∥b;④若a⊥M,b⊥M,则a∥b.其中正确命题的个数有
M,a∥b,则a∥M;③若a⊥c,b⊥c,则a∥b;④若a⊥M,b⊥M,则a∥b.其中正确命题的个数有
| A.0个 | B.1个 | C.2个 | D.3个 |
设、 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 | B.若 , ,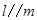 ,则 ,则 |
C.若 , , ,则 ,则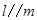 | D.若 , , ,则 ,则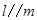 |
已知直线 a和平面?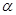 ,
,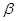 ,
,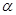 ∩
∩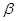 =l,a
=l,a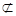
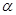 ,a
,a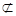
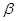 ,a在
,a在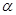 ,
,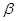 内的射影分别为直线 b 和 c ,则 b 和 c 的位置关系是( )
内的射影分别为直线 b 和 c ,则 b 和 c 的位置关系是( )
| A.相交或平行 | B.相交或异面 |
| C.平行或异面 | D.相交﹑平行或异面 |
正方体 中
中 与截面
与截面 所成的角是
所成的角是
A. | B. | C. | D. |
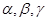 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题: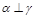 ,
,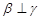 ,则
,则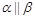 ;
;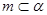 ,
,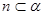 ,
,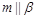 ,
,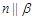 ,则
,则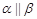 ;
;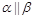 ,
,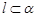 ,则
,则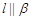 ;
;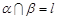 ,
,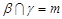 ,
,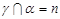 ,
,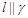 ,则
,则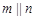 其中真命
其中真命