题目内容
从椭圆 上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )A.

B.

C.

D.

【答案】分析:依题意,可求得点P的坐标P(-c, ),由AB∥OP⇒kAB=kOP⇒b=c,从而可得答案.
),由AB∥OP⇒kAB=kOP⇒b=c,从而可得答案.
解答:解:依题意,设P(-c,y)(y>0),
则 +
+ =1,
=1,
∴y= ,
,
∴P(-c, ),
),
又A(a,0),B(0,b),AB∥OP,
∴kAB=kOP,即 =
= =
= ,
,
∴b=c.
设该椭圆的离心率为e,则e2= =
= =
= =
= ,
,
∴椭圆的离心率e= .
.
故选C.
点评:本题考查椭圆的简单性质,求得点P的坐标(-c, )是关键,考查分析与运算能力,属于中档题.
)是关键,考查分析与运算能力,属于中档题.
 ),由AB∥OP⇒kAB=kOP⇒b=c,从而可得答案.
),由AB∥OP⇒kAB=kOP⇒b=c,从而可得答案.解答:解:依题意,设P(-c,y)(y>0),
则
 +
+ =1,
=1,∴y=
 ,
,∴P(-c,
 ),
),又A(a,0),B(0,b),AB∥OP,
∴kAB=kOP,即
 =
= =
= ,
,∴b=c.
设该椭圆的离心率为e,则e2=
 =
= =
= =
= ,
,∴椭圆的离心率e=
 .
.故选C.
点评:本题考查椭圆的简单性质,求得点P的坐标(-c,
 )是关键,考查分析与运算能力,属于中档题.
)是关键,考查分析与运算能力,属于中档题. 
练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
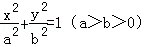 上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )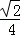 B.
B. 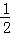 C.
C. 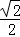 D.
D. 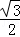
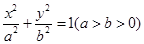 上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB//OP,
上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB//OP,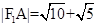 ,求椭圆的方程
,求椭圆的方程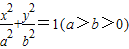 上一点P向x轴引垂线,垂足恰为椭圆的左焦点F1,A为椭圆的右顶点,B是椭圆的上顶点,且
上一点P向x轴引垂线,垂足恰为椭圆的左焦点F1,A为椭圆的右顶点,B是椭圆的上顶点,且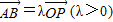 .
.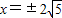 ,求椭圆方程.
,求椭圆方程.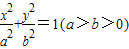 上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP(O为坐标原点),则该椭圆的离心率为( )
上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP(O为坐标原点),则该椭圆的离心率为( )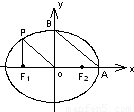

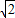

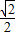
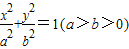 上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP,
上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP,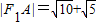 ,求椭圆的方程.
,求椭圆的方程.