题目内容
(理)对于任意x∈(0,
],不等式psin2x+cos4x≥2sin2x恒成立,则实数p的范围为______.
| π |
| 2 |
∵psin2x+cos4x≥2sin2x
∴psin2x≥2sin2x-1-sin4x+2sin2x=4sin2x-sin4x-1
∴p≥4-(sin2x+
)
而sin2x+
≥2
∴4-(sin2x+
)的最大值为2则p≥2
故答案为:[2,+∞)
∴psin2x≥2sin2x-1-sin4x+2sin2x=4sin2x-sin4x-1
∴p≥4-(sin2x+
| 1 |
| sin2x |
而sin2x+
| 1 |
| sin2x |
∴4-(sin2x+
| 1 |
| sin2x |
故答案为:[2,+∞)

练习册系列答案
相关题目
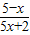 ≥0的解集是 .
≥0的解集是 .