题目内容
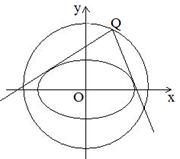
已知圆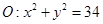 ,椭圆
,椭圆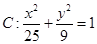 .
.
(Ⅰ)若点 在圆
在圆 上,线段
上,线段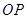 的垂直平分线经过椭圆的右焦点,求点
的垂直平分线经过椭圆的右焦点,求点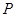 的横坐标;
的横坐标;
(Ⅱ)现有如下真命题:
“过圆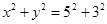 上任意一点
上任意一点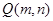 作椭圆
作椭圆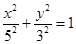 的两条切线,则这两条切线互相垂直”;
的两条切线,则这两条切线互相垂直”;
“过圆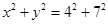 上任意一点
上任意一点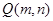 作椭圆
作椭圆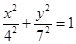 的两条切线,则这两条切线互相垂直”.
的两条切线,则这两条切线互相垂直”.
据此,写出一般结论,并加以证明.
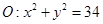 ,椭圆
,椭圆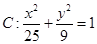 .
.(Ⅰ)若点
 在圆
在圆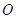 上,线段
上,线段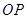 的垂直平分线经过椭圆的右焦点,求点
的垂直平分线经过椭圆的右焦点,求点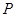 的横坐标;
的横坐标;(Ⅱ)现有如下真命题:
“过圆
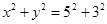 上任意一点
上任意一点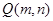 作椭圆
作椭圆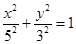 的两条切线,则这两条切线互相垂直”;
的两条切线,则这两条切线互相垂直”;“过圆
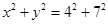 上任意一点
上任意一点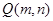 作椭圆
作椭圆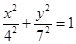 的两条切线,则这两条切线互相垂直”.
的两条切线,则这两条切线互相垂直”.据此,写出一般结论,并加以证明.
(1)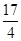
(2)一般结论为: “过圆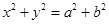 上任意一点
上任意一点 作椭圆
作椭圆 的两条切线,则这两条切线互相垂直.”
的两条切线,则这两条切线互相垂直.”
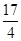
(2)一般结论为: “过圆
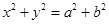 上任意一点
上任意一点 作椭圆
作椭圆 的两条切线,则这两条切线互相垂直.”
的两条切线,则这两条切线互相垂直.”试题分析:解法一:
(Ⅰ)设点
 ,则
,则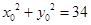 , (1) 1分
, (1) 1分
设线段
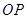 的垂直平分线与
的垂直平分线与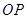 相交于点
相交于点 ,则
,则
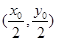 , 2分
, 2分椭圆
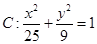 的右焦点
的右焦点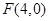 , 3分
, 3分 ,
,
 ,
,
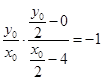 ,
,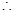
 , (2) 4分
, (2) 4分由(1),(2),解得
 ,
,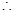 点
点 的横坐标为
的横坐标为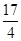 . 5分
. 5分(Ⅱ)一般结论为:
“过圆
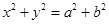 上任意一点
上任意一点 作椭圆
作椭圆 的两条切线,则这两条切线互相垂直.” 6分
的两条切线,则这两条切线互相垂直.” 6分证明如下:
(ⅰ)当过点
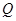 与椭圆
与椭圆 相切的一条切线的斜率
相切的一条切线的斜率不存在时,此时切线方程为
 ,
, 点
点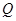 在圆
在圆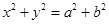 上 ,
上 ,
 ,
, 直线
直线 恰好为过点
恰好为过点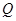 与椭圆
与椭圆 相切的另一条切线
相切的另一条切线 两切线互相垂直. 7分
两切线互相垂直. 7分(ⅱ)当过点
 与椭圆
与椭圆 相切的切线的斜率存在时,
相切的切线的斜率存在时,可设切线方程为
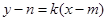 ,
,由
 得
得  ,
,整理得
 , 8分
, 8分 直线与椭圆相切,
直线与椭圆相切,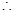
 ,
,整理得
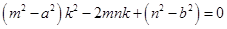 , 9分
, 9分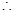
 , 10分
, 10分 点
点 在圆
在圆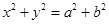 上,
上,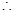
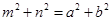 ,
, 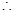
 ,
,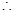
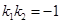 ,
,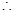 两切线互相垂直,
两切线互相垂直,综上所述,命题成立. 13分
解法二:
(Ⅰ)设点
 ,则
,则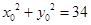 , (1) 1分
, (1) 1分椭圆
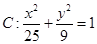 的右焦点
的右焦点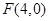 , 2分
, 2分 点
点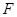 在线段
在线段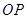 的垂直平分线上,
的垂直平分线上, 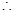
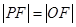 ,
,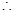
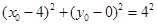 ,
, 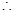
 , (2) 4分
, (2) 4分由(1),(2),解得
 ,
, 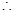 点
点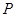 的横坐标为
的横坐标为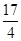 . 5分
. 5分点评:主要是考查了椭圆的性质,以及直线与椭圆的位置关系的运用,属于中档题。

练习册系列答案
相关题目
 过定点
过定点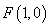 ,且与定直线
,且与定直线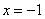 相切.
相切.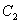 的方程;
的方程;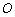 的椭圆
的椭圆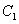 的一个焦点为
的一个焦点为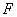 ,直线过点
,直线过点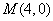 .若坐标原点
.若坐标原点 在曲线
在曲线 ,则以
,则以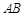 为直径的圆的方程是( )
为直径的圆的方程是( )



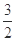 ,3)的直线,交圆
,3)的直线,交圆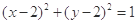 于A、B两点,Q为圆上任意一点,且Q到AB的最大距离为
于A、B两点,Q为圆上任意一点,且Q到AB的最大距离为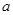 为任意实数时,直线
为任意实数时,直线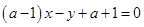 恒过定点
恒过定点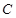 ,则以
,则以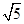 的圆是( )
的圆是( )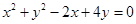



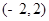 ,半径为5的圆的标准方程为( )
,半径为5的圆的标准方程为( )



 ,则该圆的半径为____________
,则该圆的半径为____________