题目内容
求函数y=x2-2x+3在x∈［-1，2）上的最大值、最小值.思路解析：函数f（x）为二次函数，在区间［-1，2］上的图象已确定，可结合图象求函数最值.
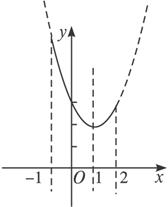
解：原函数变形为y=（x-1）2+2，x∈［-1，2］，对称轴方程为x=1.作出函数y=（x-1）2+2在x∈［-1，2］上的图象，如上图实线部分，可以看出y的最小值在x=1时取到，为2，y的最大值在x=-1时取到，为6.
练习册系列答案
考前必练系列答案
相关题目
考前必练系列答案题目内容
求函数y=x2-2x+3在x∈［-1，2）上的最大值、最小值.思路解析：函数f（x）为二次函数，在区间［-1，2］上的图象已确定，可结合图象求函数最值.
解：原函数变形为y=（x-1）2+2，x∈［-1，2］，对称轴方程为x=1.作出函数y=（x-1）2+2在x∈［-1，2］上的图象，如上图实线部分，可以看出y的最小值在x=1时取到，为2，y的最大值在x=-1时取到，为6.
考前必练系列答案