题目内容
已知入射光线所在直线的方程为2x-y-4=0,经x轴反射,那么反射光线所在直线的方程是
- A.y=-2x-4
- B.y=-2x+4
- C.
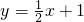
- D.
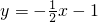
B
分析:由题意可得已知直线过点A(2,0),B(0,-4),由反射原理,反射光线必经过点A(2,0)和点B关于x轴的对称点B′(0,4),然后由求直线方程的方法可得答案.
解答: 解:由已知直线方程,令y=0可得x=2,令x=0可得y=-4,
解:由已知直线方程,令y=0可得x=2,令x=0可得y=-4,
即入射光线所在直线与x轴、y轴分别相交于点A(2,0),B(0,-4),
由反射原理,反射光线必经过点A(2,0)和点B关于x轴的对称点B′(0,4),
故可得其斜率为: =-2,由斜截式方程可得,
=-2,由斜截式方程可得,
所求反射光线所在直线方程为:y=-2x+4
故选B
点评:本题为直线方程的求解,由反射原理得出反射光线上的两个定点是解决问题的关键,属中档题.
分析:由题意可得已知直线过点A(2,0),B(0,-4),由反射原理,反射光线必经过点A(2,0)和点B关于x轴的对称点B′(0,4),然后由求直线方程的方法可得答案.
解答:
 解:由已知直线方程,令y=0可得x=2,令x=0可得y=-4,
解:由已知直线方程,令y=0可得x=2,令x=0可得y=-4,即入射光线所在直线与x轴、y轴分别相交于点A(2,0),B(0,-4),
由反射原理,反射光线必经过点A(2,0)和点B关于x轴的对称点B′(0,4),
故可得其斜率为:
 =-2,由斜截式方程可得,
=-2,由斜截式方程可得,所求反射光线所在直线方程为:y=-2x+4
故选B
点评:本题为直线方程的求解,由反射原理得出反射光线上的两个定点是解决问题的关键,属中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目

