题目内容
(本小题13分)已知函数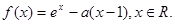
(1)若实数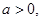 求函数
求函数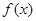 在
在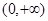 上的极值;
上的极值;
(2)记函数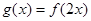 ,设函数
,设函数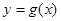 的图像
的图像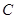 与
与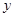 轴交于
轴交于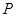 点,曲线
点,曲线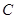 在
在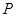 点处的切线与两坐标轴所围成图形的面积为
点处的切线与两坐标轴所围成图形的面积为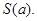 则当
则当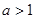 时,求
时,求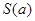 的最小值.
的最小值.
【答案】
(1)有极小值 .(2)2.
.(2)2.
【解析】
试题分析:(1)求函数的导数,然后确定函数f(x)的单调区间,在进一步求出极值即可.
(2)求出g(x)的解析式,求出P(0,1+a),由导数的几何意义求出P点处的斜率,在求出切线方程,写出S(a)的表达式,由基本不等式的性质求其最小值即可.
试题解析:(1)
当 时,由
时,由
若 ,则
,则 ,所以
,所以 恒成立,
恒成立,
所以 单调递增,无极值。
单调递增,无极值。
若 ,则
,则 单调递减;
单调递减;
 单调递增。
单调递增。
所以 有极小值
有极小值 。
。
(2) =
=
令 得
得 ,即
,即
 点处切线斜率:
点处切线斜率:
 点处切线方程:
点处切线方程:
令 得
得 ,令
,令 得
得
所以
令

当且仅当
考点:1.求函数的导数和导数的几何意义;2.利用导数求函数的单调区间;3.基本不等式的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,
 ∥
∥ 时,求
时,求 的值;
的值; 在
在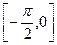 上的值域.
上的值域. 满足
满足 ,且
,且 是
是 ,
, 的等差中项.
的等差中项. ,
, ,求使
,求使
 成立的正整数
成立的正整数 的最小值.
的最小值. 过直线
过直线 和
和 的交点;
的交点;  垂直,求直线
垂直,求直线 到直线
到直线 的距离为1.求直线
的距离为1.求直线 ,过
,过 作直线
作直线 .
.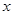 轴不垂直,交抛物线于A、B两点,是否存在
轴不垂直,交抛物线于A、B两点,是否存在 ,使得
,使得 ?若存在,求出m的值;若不存在,请说明理由?
?若存在,求出m的值;若不存在,请说明理由? 轴和
轴和 为定值,试证之;
为定值,试证之;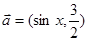 ,
,
 ∥
∥ 时,求
时,求 的值;
的值;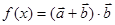 在
在 上的值域.
上的值域.