题目内容
(本小题13分)
已知抛物线方程为 ,过
,过 作直线
作直线 .
.
①若 与
与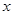 轴不垂直,交抛物线于A、B两点,是否存在
轴不垂直,交抛物线于A、B两点,是否存在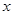 轴上一定点
轴上一定点 ,使得
,使得 ?若存在,求出m的值;若不存在,请说明理由?
?若存在,求出m的值;若不存在,请说明理由?
②若 与
与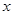 轴垂直,抛物线的任一切线与
轴垂直,抛物线的任一切线与 轴和
轴和 分别交于M、N两点,则自点M到以QN为直径的圆的切线长
分别交于M、N两点,则自点M到以QN为直径的圆的切线长 为定值,试证之;
为定值,试证之;
【答案】
(1存在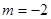
(2) 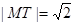
【解析】解:①设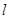 的方程为:
的方程为: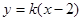 ,设
,设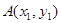 ,
,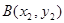
由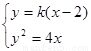 消去
消去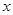 得:
得: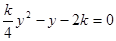 ,
,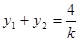 ,
,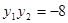 …2分
…2分
若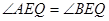 ,则
,则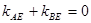 ……3分
……3分
即: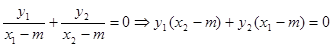 ……4分
……4分

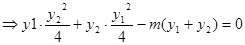
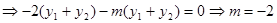 ……6分
……6分
故存在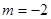 ,使得
,使得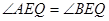 ……7分
……7分
②设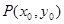 在抛物线上,由抛物线的对称性,不妨设
在抛物线上,由抛物线的对称性,不妨设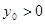 ,则过P点的切线斜率
,则过P点的切线斜率
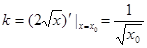 ,切线方程为:
,切线方程为: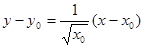 ,且
,且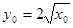 …9分
…9分
令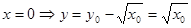 ,∴
,∴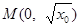
令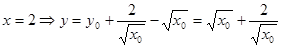 ,∴
,∴ …10分
…10分
则以QN为直径的圆的圆心坐标为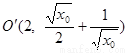 ,半径
,半径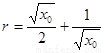 …11分
…11分
∴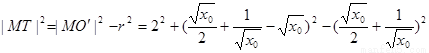
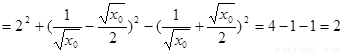
∴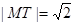 ……13分
……13分

练习册系列答案
相关题目
 ,实数a,b为常数),
,实数a,b为常数), 在(0,+∞)上是单调增函数,求b的取值范围;
在(0,+∞)上是单调增函数,求b的取值范围; 在(0,1]上解的个数。
在(0,1]上解的个数。 .
. 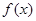 的最小正周期和当
的最小正周期和当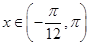 时的值域;
时的值域;
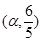 ,
,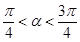 .求
.求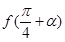 的值.
的值.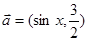 ,
,
 ∥
∥ 时,求
时,求 的值;
的值;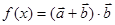 在
在 上的值域.
上的值域.