题目内容
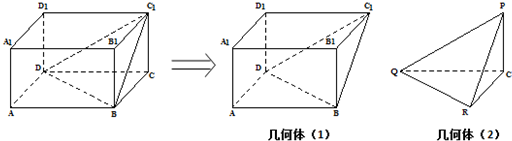
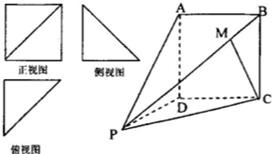
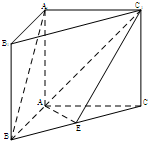
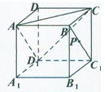
如图,在长方体ABCD-A1B1C1D1中,AB=2BC=2BB1,沿平面C1BD把这个长方体截成两个几何体:
(Ⅰ)设几何体(1)、几何体(2)的体积分为是V1、V2,求V1与V2的比值;
(Ⅱ)在几何体(2)中,求二面角P-QR-C的正切值.
(Ⅰ)设几何体(1)、几何体(2)的体积分为是V1、V2,求V1与V2的比值;
(Ⅱ)在几何体(2)中,求二面角P-QR-C的正切值.

( I)设BC=a,则AB=2a,BB1=a,
所以VABCD-A1B1C1D1=2a×a×a=2a3---------(2分)
因为V2=
S△CQR×PC=
×
×2a×a×a=
a3--------------------------(4分)V1=VABCD-A1B1C1D1-V2=2a3-
a3=
a3----------------------(5分)
所以
=
=5------------(6分)
(II)由点C作CH⊥QR于点H,连结PH,
因为PC⊥面CQR,QR?面CQR,
所以PC⊥QR.
因为PC∩CH=C,
所以QR⊥面PCH,
又因为PH?面PCH,
所以QR⊥PH,
所以∠PHC是二面角P-QR-C的平面角--------------------(9分)
而CH•QR=CQ•CR,CH×
a=a×2a,CH=
所以tan∠PHC=
=
----------------------------------------------(12分)
所以VABCD-A1B1C1D1=2a×a×a=2a3---------(2分)
因为V2=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |
所以
| V1 |
| V2 |
| ||
|
(II)由点C作CH⊥QR于点H,连结PH,
因为PC⊥面CQR,QR?面CQR,
所以PC⊥QR.
因为PC∩CH=C,
所以QR⊥面PCH,
又因为PH?面PCH,
所以QR⊥PH,
所以∠PHC是二面角P-QR-C的平面角--------------------(9分)
而CH•QR=CQ•CR,CH×
| 5 |
| 2a | ||
|
所以tan∠PHC=
| a | ||||
|
| ||
| 2 |

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
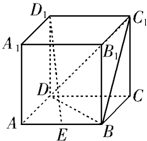
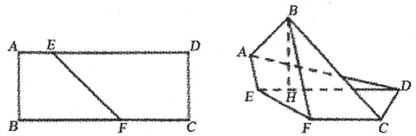
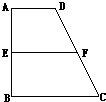 已知梯形ABCD中,AD
已知梯形ABCD中,AD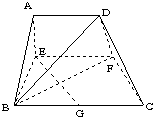
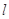 ,
,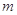 ,
,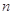 为三条不同的直线,
为三条不同的直线,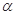 ,
,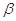 为两个不同的平面,下列命题中正确的是( )
为两个不同的平面,下列命题中正确的是( ) 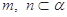 ,则
,则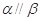 .
.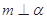 ,
,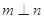 ,则
,则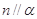 .
.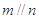 ,
,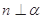 ,则
,则