题目内容
已知 ,则f(2)+f(4)+f(8)+…+f(28)的值等于______.
,则f(2)+f(4)+f(8)+…+f(28)的值等于______.
解:设2t=3x,则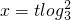 ,
,
∴f(2t)=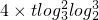 +
+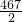 =
=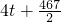 .
.
∴f(2)+f(4)+f(8)+…+f(28)=4(1+2+…+8)+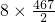 =2012.
=2012.
故答案为2012.
分析:设2t=3x,化为对数式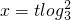 ,可得f(2t)=
,可得f(2t)=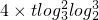 +
+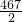 =
=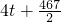 .进而即可得出答案.
.进而即可得出答案.
点评:熟练掌握换元法、指数式与对数式的互化、等差数列的前n项和等是解题的关键.
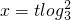 ,
,∴f(2t)=
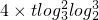 +
+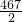 =
=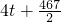 .
.∴f(2)+f(4)+f(8)+…+f(28)=4(1+2+…+8)+
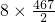 =2012.
=2012.故答案为2012.
分析:设2t=3x,化为对数式
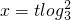 ,可得f(2t)=
,可得f(2t)=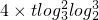 +
+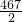 =
=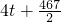 .进而即可得出答案.
.进而即可得出答案.点评:熟练掌握换元法、指数式与对数式的互化、等差数列的前n项和等是解题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
 ,则f(2)+f(-2)的值为( )
,则f(2)+f(-2)的值为( ) ,则f(2)+f(-2)的值为( )
,则f(2)+f(-2)的值为( ) ,则f(2)+f(-2)的值为( )
,则f(2)+f(-2)的值为( ) ,则f(2)+f(-2)的值为( )
,则f(2)+f(-2)的值为( )