题目内容
【题目】定义:直线关于圆的圆心距单位![]() 圆心到直线的距离与圆的半径之比.
圆心到直线的距离与圆的半径之比.
(1)设圆![]() ,求过点
,求过点![]() 的直线关于圆
的直线关于圆![]() 的圆心距单位
的圆心距单位![]() 的直线方程.
的直线方程.
(2)若圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,且直线
,且直线![]() 关于圆
关于圆![]() 的圆心距单位
的圆心距单位![]() ,求此圆
,求此圆![]() 的方程.
的方程.
(3)是否存在点![]() ,使过点
,使过点![]() 的任意两条互相垂直的直线分别关于相应两圆
的任意两条互相垂直的直线分别关于相应两圆![]() 与
与![]() 的圆心距单位始终相等?若存在,求出相应的
的圆心距单位始终相等?若存在,求出相应的![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)设过![]() 的直线方程为
的直线方程为![]() ,求得已知圆的圆心和半径,由新定义,可得方程,求得
,求得已知圆的圆心和半径,由新定义,可得方程,求得![]() ,即可得到所求直线方程;
,即可得到所求直线方程;
(2)设圆![]() 的方程为
的方程为![]() ,由题意可得
,由题意可得![]() ,①
,①![]() ②,
②,![]() ③,解方程可得
③,解方程可得![]() ,
,![]() ,
,![]() ,进而得到所求圆的方程;
,进而得到所求圆的方程;
(3)假设存在点![]() ,设过
,设过![]() 的两直线为
的两直线为![]() 和
和![]() ,求得两圆的圆心和半径,由新定义可得方程,化简整理可得
,求得两圆的圆心和半径,由新定义可得方程,化简整理可得![]() ,或
,或![]() ,再由恒成立思想可得
,再由恒成立思想可得![]() ,
,![]() 的方程,解方程可得
的方程,解方程可得![]() 的坐标.
的坐标.
解:(1)设过![]() 的直线方程为
的直线方程为![]() ,
,
圆![]() 的圆心为
的圆心为![]() ,半径为1,
,半径为1,
由题意可得![]() ,
,
解得![]() ,
,
即有所求直线为![]() ;
;
(2)设圆![]() 的方程为
的方程为![]() ,
,
由题意可得![]() ,①
,①
![]() ②,
②,![]() ③
③
解方程可得![]() ,
,![]() ,
,![]() ,或
,或![]() ,
,![]() ,
,![]() .
.
则圆![]() 的方程为
的方程为![]() 或
或![]() ;
;
(3)假设存在点![]() ,设过
,设过![]() 的两直线为
的两直线为![]() 和
和
![]() ,又
,又![]() 的圆心为
的圆心为![]() ,半径为1,
,半径为1,
![]() 的圆心为
的圆心为![]() ,半径为2,
,半径为2,
由题意可得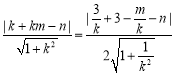 ,
,
化简可得![]() ,或
,或![]() ,
,
即有![]() 或
或![]() ,
,
解得![]() 或
或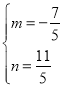 .
.
则存在这样的点![]() 和
和![]() ,使得使过
,使得使过![]() 的任意两条互相垂直的直线
的任意两条互相垂直的直线
分别关于相应两圆的距离比始终相等.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案【题目】某高校健康社团为调查本校大学生每周运动的时长,随机选取了80名学生,调查他们每周运动的总时长(单位:小时),按照![]()
![]()
![]()
![]()
![]()
![]() 共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
表1:男生
时长 |
|
|
|
|
|
|
人数 | 2 | 8 | 16 | 8 | 4 | 2 |
表2:女生
时长 |
|
|
|
|
|
|
人数 | 0 | 4 | 12 | 12 | 8 | 4 |
(1)从每周运动时长不小于20小时的男生中随机选取2人,求选到“运动达人”的概率;
(2)根据题目条件,完成下面![]() 列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
每周运动的时长小于15小时 | 每周运动的时长不小于15小时 | 总计 | |
男生 | |||
女生 | |||
总计 |
参考公式: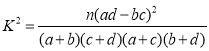 ,其中
,其中![]() .
.
参考数据:
| 0.40 | 0.25 | 0.10 | 0.010 |
| 0.708 | 1.323 | 2.706 | 6.635 |
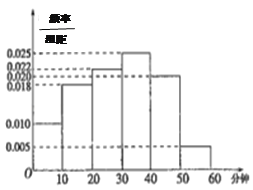
【题目】电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成上面的2×2列联表,若按95%的可靠性要求,并据此资料,你是否认为“体育迷”与性别有关?
(2)现在从该地区非体育迷的电视观众中,采用分层抽样方法选取5名观众,求从这5名观众选取两人进行访谈,被抽取的2名观众中至少有一名女生的概率.
附:![]()
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |