题目内容
17.清代著名数学家梅彀成在他的《增删算法统宗》中有这样一歌谣:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”其译文为:“远远望见7层高的古塔,每层塔点着的灯数,下层比上层成倍地增加,一共有381盏,请问塔尖几盏灯?”则按此塔各层灯盏的设置规律,从上往下数第4层的灯盏数应为( )| A. | 3 | B. | 12 | C. | 24 | D. | 36 |
分析 由题意知第七层至第一层的灯的盏数构成一个以a1为首项,以2为公比的等比数列,由等比数列的求和公式可得a1,即可求出a4.
解答 解:依题意知,此塔各层的灯盏数构成公比q=2的等比数列,且前7项和S7=381,
由 $\frac{{{a_1}(1-{2^7})}}{1-2}=381$,解得a1=3,
故${a_4}={a_1}{q^3}=24$.
故选:C.
点评 本题考查等比数列的求和公式,由题意构造等比数列是解决问题的关键,属基础题.

练习册系列答案
相关题目
5.已知A=[1,+∞),$B=\left\{{x∈R|\frac{1}{2}≤x≤2a-1}\right\}$,若A∩B≠∅,则实数a的取值范围是( )
| A. | [1,+∞) | B. | $[{\frac{1}{2},1}]$ | C. | $[{\frac{2}{3},+∞})$ | D. | (1,+∞) |
12. 如图的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )
如图的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )
 如图的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )
如图的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )| A. | 2,4 | B. | 2,5 | C. | 0,4 | D. | 0,5 |
2.已知双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$右焦点为F,P为双曲线左支上一点,点$A(0,\sqrt{2})$,则△APF周长的最小值为4(1+$\sqrt{2}$).
9.某校高三子啊一次模拟考试后,为了解数学成绩是否与班级有关,对甲乙两个班数学成绩(满分150分)进行分析,按照不小于120分为优秀,120分以下为非优秀的标准统计成绩,已知从全班100人中随机抽取1人数学成绩优秀的概率为$\frac{3}{10}$,调查结果如表所示.
(1)请完成上面的列联表;
(2)根据列联表的数据,问是否有95%的把握认为“数学成绩与班级有关系”;
(3)若按下面的方法从甲班数学成绩优秀的学生中抽取1人:把甲班数学成绩优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数和被记为抽取人的编号,求抽到的编号为6或10的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 100 |
(2)根据列联表的数据,问是否有95%的把握认为“数学成绩与班级有关系”;
(3)若按下面的方法从甲班数学成绩优秀的学生中抽取1人:把甲班数学成绩优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数和被记为抽取人的编号,求抽到的编号为6或10的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
6.已知函数f(x)=-x5-x3-5x+2,若f(a2)+f(a-2)>4,则实数a的取值范围( )
| A. | (-∞,1) | B. | (-∞,3) | C. | (-2,1) | D. | (-1,2) |
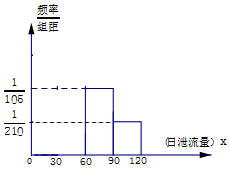 某地政府在该地一水库上建造一座水电站,用泄流水量发电,如图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知X∈[0,120],历年中日泄流量在区间[30,60)的年平均天数为156天,一年按364天计.
某地政府在该地一水库上建造一座水电站,用泄流水量发电,如图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知X∈[0,120],历年中日泄流量在区间[30,60)的年平均天数为156天,一年按364天计.