Question

已知点P₁（a₁，b₁），P₂（a₂，b₂），…，P_n（a_n，b_n）（n为正整数）都在函数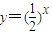图象上．
（Ⅰ）若数列{a_n}是等差数列，证明：数列{b_n}是等比数列；
（Ⅱ）设a_n=n（n为正整数），过点P_n，P_n+1的直线与两坐标轴所围成的三角形面积为c_n，试求最小的实数t，使c_n≤t对一切正整数n恒成立；
（Ⅲ）对（Ⅱ）中的数列{a_n}，对每个正整数k，在a_k与a_k+1之间插入3^k-1个3，得到一个新的数列{d_n}，设S_n是数列{d_n}的前n项和，试探究2008是否数列{S_n}中的某一项，写出你探究得到的结论并给出证明．

Answer 1

【答案】分析：（Ⅰ）若设数列{a_n}的公差为d，则，为常数，即证数列{b_n}是等比数列．
（Ⅱ）若a_n=n，则，得点，，从而得斜率，即得直线P_nP_n+1的方程，求得它与x轴，y轴的交点A_n，B_n，得数列{c_n}的通项公式，{c_n}的增减性，知，即得最小的实数t的值．
（Ⅲ）由a_n=n，知数列{d_n}中，从第一项a₁开始到a_k为止的所有项的和是（1+2+…+k）+（3¹+3²+…+3^k-1），k=7时，和是，k=8时，和是；2008-1120=888是3的倍数，所以存在自然数m，使S_m=2008；求出m的值即可．
解答：解：（Ⅰ）设数列{a_n}的公差为d，由已知，
所以，（常数），
所以，数列{b_n}是等比数列．
（Ⅱ）若a_n=n，则，
∴，，，
直线P_nP_n+1的方程为，
它与x轴，y轴分别交于点A_n（n+2，0），，
∴，
，
∴数列{c_n}随n增大而减小，
∴，即最小的实数t的值为．
（Ⅲ）∵a_n=n，∴数列{d_n}中，从第一项a₁开始到a_k为止（含a_k项）的所有项的和是：
（1+2+…+k）+（3¹+3²+…+3^k-1）=+，
当k=7时，其和是，
而当k=8时，其和是．
又因为2008-1120=888=296×3，是3的倍数，
所以存在自然数m，使S_m=2008．
此时m=7+（1+3+3²+…+3⁵）+296=667．
点评：本题考查了数列与函数的综合应用问题，解题时灵活应用了等比关系的确定，数列的求和公式等知识，是较难的题目．