题目内容
如图,在等腰梯形SBCD中,AB∥CD,且AB=2AD,设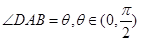 ,以A,B为焦点且过点D的双曲线离心率为
,以A,B为焦点且过点D的双曲线离心率为 ,以C,D为焦点且过点A的椭圆的离心率为
,以C,D为焦点且过点A的椭圆的离心率为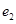 ,则( )
,则( )
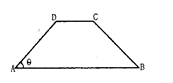
A.随着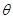 角的增大,
角的增大, 增大,
增大,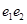 为定值
为定值
B. 随着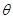 角的增大,
角的增大, 减小,
减小,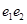 为定值
为定值
C. 随着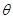 角的增大,
角的增大, 增大,
增大,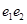 也增大
也增大
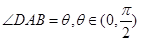 ,以A,B为焦点且过点D的双曲线离心率为
,以A,B为焦点且过点D的双曲线离心率为 ,以C,D为焦点且过点A的椭圆的离心率为
,以C,D为焦点且过点A的椭圆的离心率为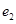 ,则( )
,则( )
A.随着
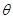 角的增大,
角的增大, 增大,
增大,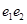 为定值
为定值 B. 随着
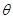 角的增大,
角的增大, 减小,
减小,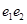 为定值
为定值C. 随着
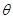 角的增大,
角的增大, 增大,
增大,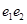 也增大
也增大B
该试题考查的知识点主要有:椭圆、双曲线及其离心率的定义,平面几何和三角函数的简单知识,函数的单调性.
思路分析:首先以角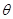 为参变量,根据椭圆和双曲线的离心率定义,结合平面几何的简单知识,把
为参变量,根据椭圆和双曲线的离心率定义,结合平面几何的简单知识,把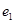 和
和 都表示为
都表示为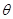 的函数.其次,根据有关函数单调性的知识(特别是复合函数的单调性知识)判别函数
的函数.其次,根据有关函数单调性的知识(特别是复合函数的单调性知识)判别函数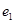 的单调性.最后,通过计算,观察
的单调性.最后,通过计算,观察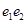 是否是常数函数,以确定
是否是常数函数,以确定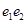 是否为定值,如果
是否为定值,如果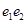 不为常数函数,还要继续考查
不为常数函数,还要继续考查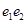 的单调性.
的单调性.
具体解答过程:由题可知:双曲线离心率 与椭圆离心率
与椭圆离心率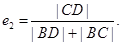
设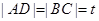 则
则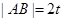 ,
,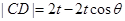 ,
, ,故
,故
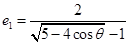 ,
, ,
,
当 时,
时,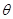 增大,
增大,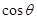 减小,导致
减小,导致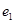 减小.
减小.
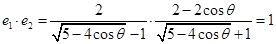 . 故选B.
. 故选B.
试题点评:从以上解题过程可以看出,该题的综合性是比较强的,要完整地做出这道题,需要考生把相关的知识点有机地结合起来,并进行适当的运算.该题属于中等难度的题.
思路分析:首先以角
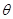 为参变量,根据椭圆和双曲线的离心率定义,结合平面几何的简单知识,把
为参变量,根据椭圆和双曲线的离心率定义,结合平面几何的简单知识,把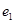 和
和 都表示为
都表示为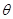 的函数.其次,根据有关函数单调性的知识(特别是复合函数的单调性知识)判别函数
的函数.其次,根据有关函数单调性的知识(特别是复合函数的单调性知识)判别函数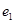 的单调性.最后,通过计算,观察
的单调性.最后,通过计算,观察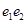 是否是常数函数,以确定
是否是常数函数,以确定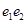 是否为定值,如果
是否为定值,如果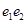 不为常数函数,还要继续考查
不为常数函数,还要继续考查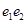 的单调性.
的单调性.具体解答过程:由题可知:双曲线离心率
 与椭圆离心率
与椭圆离心率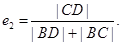
设
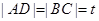 则
则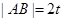 ,
,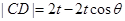 ,
, ,故
,故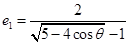 ,
, ,
,当
 时,
时,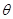 增大,
增大,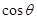 减小,导致
减小,导致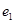 减小.
减小.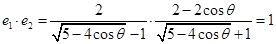 . 故选B.
. 故选B.试题点评:从以上解题过程可以看出,该题的综合性是比较强的,要完整地做出这道题,需要考生把相关的知识点有机地结合起来,并进行适当的运算.该题属于中等难度的题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
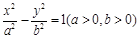 与直线
与直线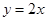 无交点,则离心率
无交点,则离心率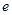 的取值范围是
的取值范围是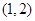
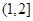
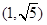
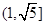
 :
: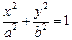 (
(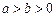 )的离心率
)的离心率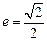 ,左、右焦点分别为
,左、右焦点分别为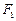 、
、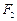 ,点
,点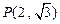 满足:
满足: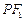 的中垂线上.
的中垂线上.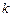 (
(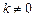 )的直线
)的直线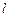 与
与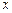 轴、椭圆
轴、椭圆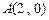 、
、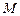 、
、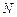 ,且
,且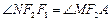 ,求
,求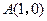 、
、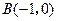 ,已知
,已知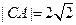 ,
,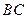 的垂直平分线
的垂直平分线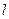 交
交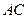 于
于 ,当点
,当点 为动点时,点
为动点时,点 .
.
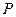 为
为 为坐标原点,曲线
为坐标原点,曲线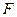 ,求
,求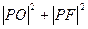 的最小值.
的最小值.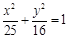 的离心率为
的离心率为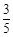
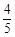
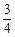
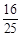
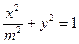 (常数
(常数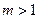 ),P是曲线C上的动点,M是曲线C的右
),P是曲线C上的动点,M是曲线C的右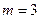 ,求|PA|的最大值与最小值.
,求|PA|的最大值与最小值.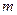 的取值范围.
的取值范围.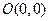 、
、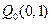 和
和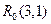 ,记
,记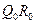 的中点为
的中点为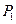 ,取
,取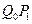 和
和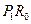 中的一条,记其端点为
中的一条,记其端点为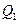 、
、 ,使之满足
,使之满足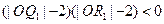 ;记
;记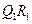 的中点为
的中点为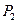 ,取
,取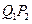 和
和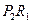 中的一条,记其端点为
中的一条,记其端点为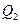 、
、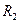 ,使之满足
,使之满足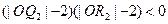 ;依次下去,得到点
;依次下去,得到点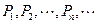 ,则
,则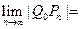 。
。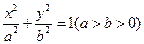 上,F1、F2分别
上,F1、F2分别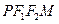 为菱形,则椭圆的离心率是
为菱形,则椭圆的离心率是 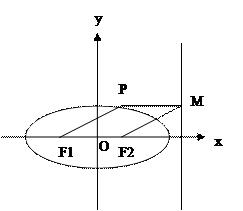
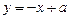 与曲线
与曲线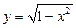 有两个交点,则
有两个交点,则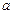 的取值范围是 .
的取值范围是 .