题目内容
设函数 .
.
(1)当a=2时,求函数f(x)的最小值;
(2)当0<a<1时,试判断函数f(x)的单调性,并证明.
解:(1)当a=2时, .
.
 .
.
当且仅当 ,即
,即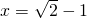 时取等号,
时取等号,
∴ .
.
(2)当0<a<1时,任取0≤x1<x2 .
.
∵0<a<1,(x1+1)(x2+1)>1,
∴ .
.
∵x1<x2,∴f(x1)<f(x2),即f(x)在[0,+∞)上为增函数.
分析:(1)当a=2时,将函数f(x)变形成 ,然后利用均值不等式即可求出函数f(x)的最小值;
,然后利用均值不等式即可求出函数f(x)的最小值;
(2)先取值任取0≤x1<x2然后作差f(x1)-f(x2),判定其符号即可判定函数f(x)在[0,+∞)上的单调性.
点评:本题主要考查了函数的最值的求解,以及函数单调性的判断与证明,同时考查了计算能力,属于基础题.
 .
. .
.当且仅当
 ,即
,即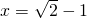 时取等号,
时取等号,∴
 .
.(2)当0<a<1时,任取0≤x1<x2
 .
.∵0<a<1,(x1+1)(x2+1)>1,
∴
 .
.∵x1<x2,∴f(x1)<f(x2),即f(x)在[0,+∞)上为增函数.
分析:(1)当a=2时,将函数f(x)变形成
 ,然后利用均值不等式即可求出函数f(x)的最小值;
,然后利用均值不等式即可求出函数f(x)的最小值;(2)先取值任取0≤x1<x2然后作差f(x1)-f(x2),判定其符号即可判定函数f(x)在[0,+∞)上的单调性.
点评:本题主要考查了函数的最值的求解,以及函数单调性的判断与证明,同时考查了计算能力,属于基础题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 。
。 的极值;
的极值; 2时,讨论函数
2时,讨论函数 成立,求
成立,求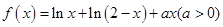 。
。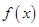 的单调区间。
的单调区间。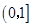 上的最大值为
上的最大值为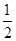 ,求a的值。
,求a的值。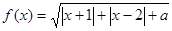 。
。 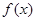 的定义域。
的定义域。 。
。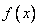 的单调区间。
的单调区间。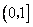 上的最大值为
上的最大值为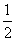 ,求a的值。
,求a的值。