题目内容
定义域为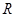 的奇函数
的奇函数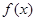 满足
满足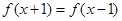 ,且当
,且当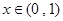 时,
时,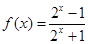 .
.
(Ⅰ)求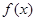 在
在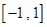 上的解析式;
上的解析式;
(Ⅱ)若存在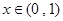 ,满足
,满足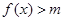 ,求实数
,求实数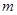 的取值范围.
的取值范围.
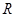 的奇函数
的奇函数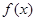 满足
满足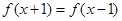 ,且当
,且当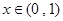 时,
时,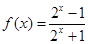 .
.(Ⅰ)求
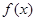 在
在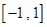 上的解析式;
上的解析式;(Ⅱ)若存在
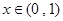 ,满足
,满足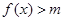 ,求实数
,求实数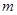 的取值范围.
的取值范围.(Ⅰ) ;(Ⅱ)实数
;(Ⅱ)实数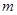 的取值范围为
的取值范围为 .
.
 ;(Ⅱ)实数
;(Ⅱ)实数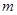 的取值范围为
的取值范围为 .
.试题分析:(Ⅰ)由已知条件:当
 时,
时,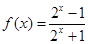 ,利用区间转换法来求函数
,利用区间转换法来求函数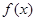 在
在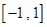 上的解析式.当
上的解析式.当 时,
时, ,由已知条件
,由已知条件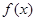 为
为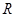 上的奇函数,得
上的奇函数,得 ,化简即可.又
,化简即可.又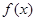 为
为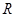 上的奇函数,可得
上的奇函数,可得 ;在已知式
;在已知式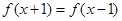 中令
中令 ,可得
,可得 又
又 由此可得
由此可得 和
和 的值,最后可得
的值,最后可得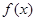 在
在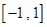 上的解析式;(Ⅱ)由已知条件:存在
上的解析式;(Ⅱ)由已知条件:存在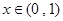 ,满足
,满足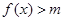 ,先利用分离常数法,求出函数
,先利用分离常数法,求出函数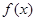 的值域,最后由:
的值域,最后由: ,即可求得实数
,即可求得实数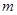 的取值范围.
的取值范围.试题解析:(Ⅰ)当
 时,
时, ,由
,由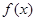 为
为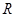 上的奇函数,得
上的奇函数,得 ,∴
,∴ . 4分
. 4分又由奇函数得
 ,
, ,
, . 7分
. 7分 . 8分
. 8分(Ⅱ)
 ,
, , 10分
, 10分
 ,
, .若存在
.若存在 ,满足
,满足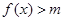 ,则
,则 ,实数
,实数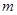 的取值范围为
的取值范围为 . 13分
. 13分
练习册系列答案
相关题目
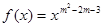 (
(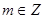 )在
)在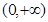 是单调减函数,且为偶函数.
是单调减函数,且为偶函数.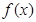 的解析式;
的解析式; 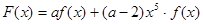 的奇偶性,并说明理由.
的奇偶性,并说明理由.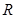 上的奇函数
上的奇函数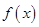 ,当
,当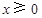 时,
时,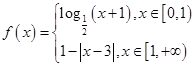 ,则方程
,则方程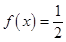 的所有解之和为 .
的所有解之和为 . 是
是 上的奇函数,
上的奇函数, 是
是 ,且
,且 ,则
,则 的值为___________.
的值为___________.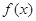 的定义域为R,
的定义域为R,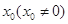 是
是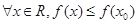
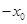 是
是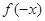 的极小值点
的极小值点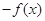 的极小值点
的极小值点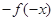 的极小值点
的极小值点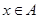 ,
,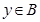 ,(
,(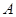 、
、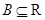 )有唯一确定的
)有唯一确定的 与之对应,称
与之对应,称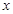 、
、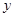 的二元函数.现定义满足下列性质的二元函数
的二元函数.现定义满足下列性质的二元函数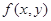 为关于实数
为关于实数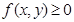 ,当且仅当
,当且仅当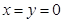 时取等号;
时取等号;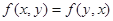 ;
;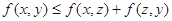 对任意的实数z均成立.
对任意的实数z均成立.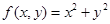 ;②
;②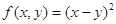 ;③
;③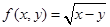 ;
;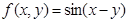 .能够成为关于的
.能够成为关于的 满足
满足 ,当
,当 时,
时, ,则
,则 ( )
( )



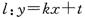 (k为常数)与正六边形交于M、N两点,记
(k为常数)与正六边形交于M、N两点,记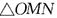 的面积为S,则关于函数
的面积为S,则关于函数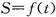 的奇偶性的判断正确的是 ( )
的奇偶性的判断正确的是 ( )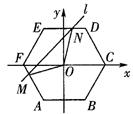
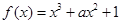 的导函数为偶函数,则
的导函数为偶函数,则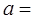 ( )
( )