题目内容

已知：sinα+sinβ+sinγ=0，且cosα+cosβ+cosγ=0.

求证：cos(α-β).

证明：由已知可得sinα+sinβ=-sinγ，cosα+cosβ=-cosγ.

两式平方相加得到2+2cos(α-β)=1，

所以cos(α-β)=，得证.

练习册系列答案
相关题目
已知向量
a
=(sinθ，1)，
b
=（-1，cosθ），
a
•
b
=-
2
，0＜θ＜π．
（Ⅰ）求θ；
（Ⅱ）求sin(
θ
2
+
π
4
)的值．
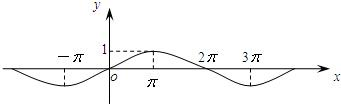精英家教网已知函数y=sinωx（ω＞0）的图象如图所示，把y=sinωx的图象向右平移
2π
3
个单位得到函数y=f（x）的图象，则f（x）=（　　）
A、sin(2x-
2π
3
)
B、sin(2x-
4π
3
)
C、sin(
1
2
x-
2π
3
)
D、sin(
1
2
x-
π
3
)
已知角α满足sinα+cosα＞0，tanα-sinα＜0，则角α的范围可能是（　　）
A、（0，
π
4
）
B、（
π
4
，
π
2
）
C、（
π
2
，
3π
4
）
D、（
3π
4
，π?）
已知f(x)=sin(x+
π
2
)，g（x）=sinx，下列选项正确的是（　　）
已知f(x)=sin(x+
π
6
)-tanα•cosx，且f(
π
3
)=
1
2
．
（1）求tanα的值；
（2）当x∈[
π
2
，π]时，求函数f（x）的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网