题目内容
下列说法:①函数
 的单调增区间是(-∞,1);
的单调增区间是(-∞,1);②若函数y=f(x)定义域为R且满足f(1-x)=f(x+1),则它的图象关于y轴对称;
③函数f(x)=
 (x∈R)的值域为(-1,1);
(x∈R)的值域为(-1,1);④函数y=|3-x2|的图象和直线y=a(a∈R)的公共点个数是m,则m的值可能是0,2,3,4;
⑤若函数f(x)=x2-2ax+5(a>1)在x∈[1,3]上有零点,则实数a的取值范围是
 .
.其中正确的序号是 .
【答案】分析:根据当x=0时,函数的解析式无意义可判断①;根据函数对称性,可得函数y=f(x)的图象关于直线x=1对称,可判断②;画出函数f(x)=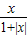 (x∈R)的图象,结合函数图象分析出函数的值域,可判断③;画出函数y=|3-x2|的图象,可分析出函数y=|3-x2|的图象和直线y=a(a∈R)的公共点个数,可判断④;根据二次函数的图象和性质分析出函数f(x)=x2-2ax+5(a>1)在x∈[1,3]上有零点,实数a的取值范围,可判断⑤.
(x∈R)的图象,结合函数图象分析出函数的值域,可判断③;画出函数y=|3-x2|的图象,可分析出函数y=|3-x2|的图象和直线y=a(a∈R)的公共点个数,可判断④;根据二次函数的图象和性质分析出函数f(x)=x2-2ax+5(a>1)在x∈[1,3]上有零点,实数a的取值范围,可判断⑤.
解答: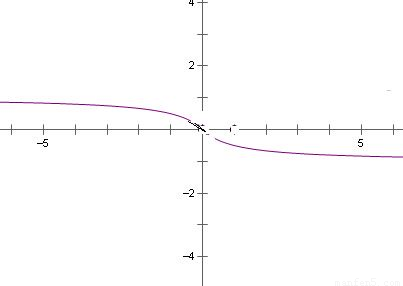 解:当x=0时,x2-2x-3=-3,此时
解:当x=0时,x2-2x-3=-3,此时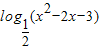 无意义,故①错误;
无意义,故①错误;
若函数y=f(x)满足f(1-x)=f(x+1),则函数y=f(x)的图象关于直线x=1对称,故②错误;
画出函数f(x)=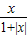 (x∈R)的图象如图,由图可得函数的值域为(-1,1);
(x∈R)的图象如图,由图可得函数的值域为(-1,1);
画出函数y=|3-x2|的图象,由图可知,函数y=|3-x2|的图象和直线y=a公共点可能是0,2,3,4个,故④正确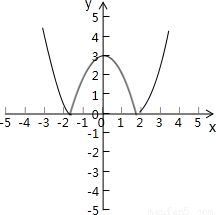
若f(x)在x∈[1,3]上有零点,则f(x)=0在x∈[1,3]上有实数解
∴2a=x+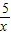 在x∈[1,3]上有实数解
在x∈[1,3]上有实数解
令g(x)=x+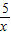 则g(x)在[1,
则g(x)在[1,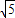 ]单调递减,在(
]单调递减,在(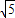 ,3]单调递增且g(1)=6,g(3)=
,3]单调递增且g(1)=6,g(3)=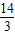 ,∴2
,∴2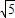 ≤g(x)≤6,即2
≤g(x)≤6,即2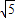 ≤2a≤6,故
≤2a≤6,故  ≤a≤3故⑤正确
≤a≤3故⑤正确
故答案为:③④⑤
点评:本题考查的知识点是复合函数的单调性,函数的对称性,函数的值域,函数图象的交点,函数的零点,是函数内容的综合应用,难度中档.
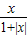 (x∈R)的图象,结合函数图象分析出函数的值域,可判断③;画出函数y=|3-x2|的图象,可分析出函数y=|3-x2|的图象和直线y=a(a∈R)的公共点个数,可判断④;根据二次函数的图象和性质分析出函数f(x)=x2-2ax+5(a>1)在x∈[1,3]上有零点,实数a的取值范围,可判断⑤.
(x∈R)的图象,结合函数图象分析出函数的值域,可判断③;画出函数y=|3-x2|的图象,可分析出函数y=|3-x2|的图象和直线y=a(a∈R)的公共点个数,可判断④;根据二次函数的图象和性质分析出函数f(x)=x2-2ax+5(a>1)在x∈[1,3]上有零点,实数a的取值范围,可判断⑤.解答:
 解:当x=0时,x2-2x-3=-3,此时
解:当x=0时,x2-2x-3=-3,此时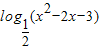 无意义,故①错误;
无意义,故①错误;若函数y=f(x)满足f(1-x)=f(x+1),则函数y=f(x)的图象关于直线x=1对称,故②错误;
画出函数f(x)=
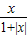 (x∈R)的图象如图,由图可得函数的值域为(-1,1);
(x∈R)的图象如图,由图可得函数的值域为(-1,1);画出函数y=|3-x2|的图象,由图可知,函数y=|3-x2|的图象和直线y=a公共点可能是0,2,3,4个,故④正确

若f(x)在x∈[1,3]上有零点,则f(x)=0在x∈[1,3]上有实数解
∴2a=x+
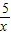 在x∈[1,3]上有实数解
在x∈[1,3]上有实数解令g(x)=x+
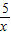 则g(x)在[1,
则g(x)在[1,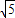 ]单调递减,在(
]单调递减,在(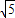 ,3]单调递增且g(1)=6,g(3)=
,3]单调递增且g(1)=6,g(3)=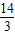 ,∴2
,∴2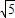 ≤g(x)≤6,即2
≤g(x)≤6,即2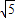 ≤2a≤6,故
≤2a≤6,故  ≤a≤3故⑤正确
≤a≤3故⑤正确故答案为:③④⑤
点评:本题考查的知识点是复合函数的单调性,函数的对称性,函数的值域,函数图象的交点,函数的零点,是函数内容的综合应用,难度中档.

练习册系列答案
相关题目
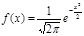 ,下列说法不正确的是
,下列说法不正确的是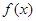 为偶函数
为偶函数 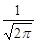
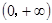 上是单调减函数,在
上是单调减函数,在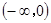 上是单调增函数
上是单调增函数  在R上是减函数
在R上是减函数