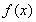题目内容
关于函数的单调性，下列说法正确的是（ ）
分析：根据二次函数的图象和性质，可判断A，B，D的真假；根据反比例函数的图象和性质，可判断C的真假．
解答：解：f（x）=x2+1在（-∞，0）上是减函数，故A错误；
f（x）=x2+1在（-∞，0）上是减函数，（-∞，-5）⊆（-∞，0），故f（x）=x2+1在（-∞，-5）上是减函数，故B正确；
f(x)=
在（-∞，0）和（0，+∞）上是减函数，但在R上不是单调函数，故C错误；
f（x）=x2+1在（-5，0）上是减函数，故D错误
故选B
f（x）=x2+1在（-∞，0）上是减函数，（-∞，-5）⊆（-∞，0），故f（x）=x2+1在（-∞，-5）上是减函数，故B正确；
f(x)=
| 1 |
| x |
f（x）=x2+1在（-5，0）上是减函数，故D错误
故选B
点评：本题考查的知识点是函数单调性的判断与证明，熟练掌握二次函数的图象和性质及反比例函数的图象和性质是解答的关键．
练习册系列答案
相关题目
所在直线为x轴，建立如图所示的直角坐标系．设
，点F的坐标为
，点G的坐标为
．
关于t的函数
的表达式，判断函数
的单调性，并证明你的判断．
的面积
，若以O为中心，F为焦点的椭圆经过点G，求当
取得最小值时椭圆的方程．
是椭圆上的两点，且
，求实数
的取值范围．
所在直线为
轴，建立如 所示的坐标系。设
，点F的坐标为
，
，点G的坐标为
。
关于
的函数
的表达式，判断函数
的单调性，并证明你的判断；
，若以O为中心，F为焦点的椭圆经过点G，求当
取最小值时椭圆的方程；
，C、D是椭圆上的两点，且
，求实数
的取值范围。
