题目内容
(本题15分)
已知直线l的方程为![]() ,且直线l与x轴交于点
,且直线l与x轴交于点![]() ,圆
,圆![]() 与x轴交于
与x轴交于![]() 两点.
两点.
(1)过M点的直线![]() 交圆于
交圆于![]() 两点,且圆孤
两点,且圆孤![]() 恰为圆周的
恰为圆周的![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)求以l为准线,中心在原点,且与圆O恰有两个公共点的椭圆方程;
 (3)过M点作直线
(3)过M点作直线![]() 与圆相切于点
与圆相切于点![]() ,设(2)中椭圆的两个焦点分别为
,设(2)中椭圆的两个焦点分别为![]() ,求三角形
,求三角形![]() 面积.
面积.
解:(1)![]() 为圆周的
为圆周的![]()
![]() 点到直线
点到直线![]() 的距离为
的距离为![]() …………2分
…………2分
设![]() 的方程为
的方程为![]()
![]() 的方程为
的方程为![]() ………………………5分
………………………5分
(2)设椭圆方程为![]() ,半焦距为c,则
,半焦距为c,则![]()
![]() 椭圆与圆O恰有两个不同的公共点,根据椭圆与圆的对称性
椭圆与圆O恰有两个不同的公共点,根据椭圆与圆的对称性
则![]() 或
或![]() ………………………6分
………………………6分
当![]() 时,
时,![]() 所求椭圆方程为
所求椭圆方程为![]() ;……………8分
;……………8分
当![]() 时,
时,![]()
所求椭圆方程为![]() ………………………10分
………………………10分
(3)设切点为N,则由题意得,在![]() 中,
中,![]() ,则
,则![]() ,
,
 N点的坐标为
N点的坐标为![]() ,……………… 11分
,……………… 11分
若椭圆为![]() 其焦点F1,F2
其焦点F1,F2
分别为点A,B故![]() , ………………………13分
, ………………………13分
若椭圆为![]() ,其焦点为
,其焦点为![]() ,
,
此时![]() ………………………15分
………………………15分

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
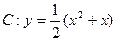 ,点
,点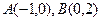 ,点E是曲线C上的一个动点(E不在直线AB上),设
,点E是曲线C上的一个动点(E不在直线AB上),设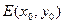 ,C,D在直线AB上,
,C,D在直线AB上,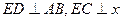 轴。
轴。 表示
表示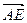 在
在 方向上的投影;
方向上的投影;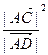 是否为定值?若是,求此定值,若不是,说明理由。
是否为定值?若是,求此定值,若不是,说明理由。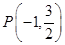 是椭圆E:
是椭圆E: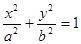 (
(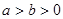 )上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.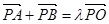 (
(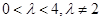 ).求证:直线AB的斜率为定值;
).求证:直线AB的斜率为定值;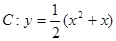 ,点
,点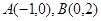 ,点E是曲线C上的一个动点(E不在直线AB上),设
,点E是曲线C上的一个动点(E不在直线AB上),设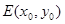 ,C,D在直线AB上,
,C,D在直线AB上,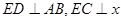 轴。
轴。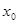 表示
表示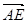 在
在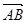 方向上的投影;
方向上的投影;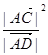 是否为定值?若是,求此定值,若不是,说明理由。
是否为定值?若是,求此定值,若不是,说明理由。