题目内容
用五种不同的颜色给图中的“五角星”的五个顶点染色，（每点染一色，有的颜色也可以不用）使每条线段上的两个顶点皆不同色，则不同的染色方法有________种．
1020
分析：可将这一问题转化为具有五个扇形格的圆盘染五色，使邻格不同色的染色问题．利用k个扇形格的圆盘染五色的方法数
的递推公式即可得本题结果
解答：
解：将其转化为具有五个扇形格的
圆盘染五色，使邻格不同色的染色问题．
设有k个扇形格的圆盘染五色的方法数
为xk，则有xk+xk-1=5•4k-1，
于是x5=（x5+x4）-（x4+x3）+（x3+x2）-x2=5（44-43+42-4）=1020
故答案为1020
点评：本题考查了分类计数原理在排列组合问题中的应用．
分析：可将这一问题转化为具有五个扇形格的圆盘染五色，使邻格不同色的染色问题．利用k个扇形格的圆盘染五色的方法数
的递推公式即可得本题结果
解答：
解：将其转化为具有五个扇形格的圆盘染五色，使邻格不同色的染色问题．
设有k个扇形格的圆盘染五色的方法数
为xk，则有xk+xk-1=5•4k-1，
于是x5=（x5+x4）-（x4+x3）+（x3+x2）-x2=5（44-43+42-4）=1020
故答案为1020
点评：本题考查了分类计数原理在排列组合问题中的应用．
练习册系列答案
相关题目
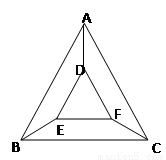
如图，用五种不同的颜色给图中的A、B、C、D、E、F六个不同的点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同的颜色，则不同的涂色方法共（ ）种．
用五种不同的颜色给图中的“五角星”的五个顶点染色，（每点染一色，有的颜色也可以不用）使每条线段上的两个顶点皆不同色，则不同的染色方法有
