题目内容
已知等比数列 的公比为
的公比为 ,
, 是
是 的前
的前 项和.
项和.
(1)若 ,
, ,求
,求 的值;
的值;
(2)若 ,
, ,
, 有无最值?并说明理由;
有无最值?并说明理由;
(3)设 ,若首项
,若首项 和
和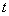 都是正整数,
都是正整数,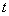 满足不等式:
满足不等式: ,且对于任意正整数
,且对于任意正整数 有
有 成立,问:这样的数列
成立,问:这样的数列 有几个?
有几个?
(1) ;(2)
;(2) 有最大值为
有最大值为 ,最小值为
,最小值为 ;(3)
;(3) 个.
个.
【解析】
试题分析:(1)根据等比数列前 项和公式
项和公式 ,可见要对
,可见要对 分类讨论,当
分类讨论,当 时,
时, ,
, ,
, ,从而不难求出
,从而不难求出 ;当
;当 时,
时, ,
, ,
, (2)若
(2)若 ,
, ,则
,则 ,
,
当 时,
时, ,所以
,所以 随
随 的增大而增大,
的增大而增大,
而 ,此时
,此时 有最小值为1,但无最大值. 6分
有最小值为1,但无最大值. 6分
当 时,
时,
① 时,
时, ,所以
,所以 随
随 的增大而增大,
的增大而增大,
即 是偶数时,
是偶数时, ,即:
,即: ; 8分
; 8分
 由此得:共有
由此得:共有 个. 18分
个. 18分

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 ,给出它的以下四个结论:①最小正周期为
,给出它的以下四个结论:①最小正周期为 ;②图像可由
;②图像可由 的图像先向左平移
的图像先向左平移 个单位长度,再把所得图像上各点的横坐标变为原来的
个单位长度,再把所得图像上各点的横坐标变为原来的 倍(纵坐标不变)而得到;③图像关于点
倍(纵坐标不变)而得到;③图像关于点 对称;④图像关于直线
对称;④图像关于直线 对称 .
对称 . 且
且 ,则
,则 的最小值为________.
的最小值为________. ,
, ,则
,则 的取值范围为___________.
的取值范围为___________. ,其中
,其中 为已知实数,
为已知实数, ,则下列各命题中错误的是…( )
,则下列各命题中错误的是…( ) .若
.若 ,则
,则 对任意实数恒成立;
对任意实数恒成立;  .若
.若 ,则函数
,则函数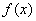 为奇函数;
为奇函数; 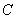 .若
.若 ,则函数
,则函数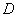 .当
.当 时,若
时,若 ,则
,则
 ,
,  ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( ) (B)
(B)  (C)
(C)  (D)
(D) 
 具有以下性质:①
具有以下性质:① ,
, ;②若
;②若 ,则
,则 ,且
,且 时,
时, .则称集合
.则称集合 _
_ ___.
___.
 中,
中, 若
若 ,则
,则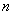 的最小值为
的最小值为 