题目内容
在△ABC中,已知A=135°,B=15°,c=2,则△ABC中最长边的长为 .
【答案】分析:由大边对大角可得最长边为a,利用正弦定理及三角形内角和定理求得a=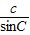 •sinA 的值.
•sinA 的值.
解答:解:由题意可得最长边为a,利用正弦定理及三角形内角和定理求得a=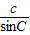 •sinA sinA=
•sinA sinA=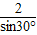 ×sin135°=2
×sin135°=2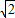 .
.
故答案为:2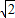 .
.
点评:本题主要考查正弦定理的应用,三角形的内角和公式,以及大边对大角,属于中档题.
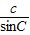 •sinA 的值.
•sinA 的值.解答:解:由题意可得最长边为a,利用正弦定理及三角形内角和定理求得a=
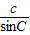 •sinA sinA=
•sinA sinA=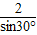 ×sin135°=2
×sin135°=2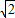 .
.故答案为:2
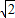 .
.点评:本题主要考查正弦定理的应用,三角形的内角和公式,以及大边对大角,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目