题目内容
5．已知正四面体ABCD（各面均为正三角形）的棱长为2，其内切球面上有一动点P，则AP的最小值为（ ）| A． | $\frac{\sqrt{6}}{3}$ | B． | $\frac{2\sqrt{6}}{3}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
分析 求出正四面体的高，进一步得到内切球的半径，由高减去内切球的直径得答案．
解答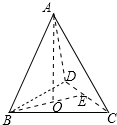 
解：设正四面体ABCD的棱长为a，高为h，每一个面的面积为S，其内切球的半径为r，
则由等积法可得，$\frac{1}{3}Sh=4•\frac{1}{3}Sr$，即$r=\frac{1}{4}h$．
正四面体ABCD的棱长为2，如图，
则BE=$\sqrt{3}$，BO=$\frac{2\sqrt{3}}{3}$，
∴$AO=\sqrt{{2}^{2}-（\frac{2\sqrt{3}}{3}）^{2}}=\frac{2\sqrt{6}}{3}$，
∴正四面体内切球的直径为$\frac{\sqrt{6}}{3}$，
则AP的最小值为$\frac{2\sqrt{6}}{3}-\frac{\sqrt{6}}{3}=\frac{\sqrt{6}}{3}$．
故选：A．
点评 本题考查棱锥的结构特征，应熟记正四面体内切球的半径是正四面体高的四分之一这一结论，是中档题．
练习册系列答案
相关题目
已知中心在坐标原点O的椭圆C经过点A（2，3），且点F（2，0）为其右焦点．
10．执行如图所示的程序框图，若输出的a等于341，则判断框内应填写（ ）
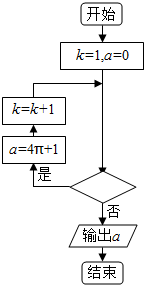
| A． | k＜4？ | B． | k＜5？ | C． | k＜6？ | D． | k＜7？ |
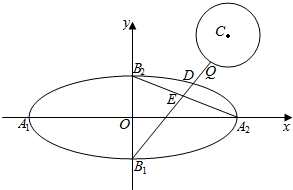如图，已知椭圆$\frac{{x}^{2}}{2}$+y2=1的四个顶点分别为A1，A2，B1，B2，左右焦点分别为F1，F2，若圆C：（x-3）2+（y-3）2=r2（0＜r＜3）上有且只有一个点P满足$\frac{|P{F}_{1}|}{|P{F}_{2}|}$=$\sqrt{5}$．