题目内容
P(x,y)是(x-3)2+y2=4上的点,则 的范围是 .如果圆(x-1)2+(y-b)2=2被x轴截得的弦长是2,那么b= .
的范围是 .如果圆(x-1)2+(y-b)2=2被x轴截得的弦长是2,那么b= .
【答案】分析:① 表示圆(x-3)2+y2=4上的动点P(x,y)与原点连线的斜率,画出满足条件的图象,分析后可得答案.
表示圆(x-3)2+y2=4上的动点P(x,y)与原点连线的斜率,画出满足条件的图象,分析后可得答案.
②先把y=0代入(x-1)2+(y-b)2=2求出对应的x,即可求出被x轴截得的弦长,再结合已知条件即可求出b.
解答:解:① 表示圆(x-3)2+y2=4上的动点P(x,y)与原点连线的斜率,
表示圆(x-3)2+y2=4上的动点P(x,y)与原点连线的斜率,
如下图所示:

设OP为y=kx,联立(x-3)2+y2=4
得(k2+1)x2+-6x+5=0
令△=36-20(k2+1)=0
解得k=±
则 的范围是[-
的范围是[- ,
, ]
]
②把y=0代入(x-1)2+(y-b)2=2得:
(x-1)2+b2=2⇒(x-1)2=2-b2⇒x1=1+ ,x2=1-
,x2=1-
所以有:|x1-x2|=2
由题得:2 =2⇒
=2⇒ =1⇒b=±1.
=1⇒b=±1.
故答案为:[- ,
, ],±1.
],±1.
点评:本题考查的知识点是直线与圆的位置关系,直线的斜率,其中第一空的关键是分析出 表示圆(x-3)2+y2=4上的动点P(x,y)与原点连线的斜率,第二空的关键是构造关于b的方程.
表示圆(x-3)2+y2=4上的动点P(x,y)与原点连线的斜率,第二空的关键是构造关于b的方程.
 表示圆(x-3)2+y2=4上的动点P(x,y)与原点连线的斜率,画出满足条件的图象,分析后可得答案.
表示圆(x-3)2+y2=4上的动点P(x,y)与原点连线的斜率,画出满足条件的图象,分析后可得答案.②先把y=0代入(x-1)2+(y-b)2=2求出对应的x,即可求出被x轴截得的弦长,再结合已知条件即可求出b.
解答:解:①
 表示圆(x-3)2+y2=4上的动点P(x,y)与原点连线的斜率,
表示圆(x-3)2+y2=4上的动点P(x,y)与原点连线的斜率,如下图所示:

设OP为y=kx,联立(x-3)2+y2=4
得(k2+1)x2+-6x+5=0
令△=36-20(k2+1)=0
解得k=±

则
 的范围是[-
的范围是[- ,
, ]
]②把y=0代入(x-1)2+(y-b)2=2得:
(x-1)2+b2=2⇒(x-1)2=2-b2⇒x1=1+
 ,x2=1-
,x2=1-
所以有:|x1-x2|=2

由题得:2
 =2⇒
=2⇒ =1⇒b=±1.
=1⇒b=±1.故答案为:[-
 ,
, ],±1.
],±1.点评:本题考查的知识点是直线与圆的位置关系,直线的斜率,其中第一空的关键是分析出
 表示圆(x-3)2+y2=4上的动点P(x,y)与原点连线的斜率,第二空的关键是构造关于b的方程.
表示圆(x-3)2+y2=4上的动点P(x,y)与原点连线的斜率,第二空的关键是构造关于b的方程. 
练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
设过点P(x,y)的直线分别与x轴的正半轴和y轴的正半轴交于A,B两点,点Q与点P关于y轴对称,O为坐标原点,若
=2
且
•
=1,则点P的轨迹方程是( )
| BP |
| PA |
| OQ |
| AB |
A、3x2+
| ||
B、3x2-
| ||
C、
| ||
D、
|
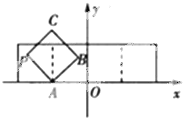 如图放置的边长为1的正方形PABC沿x轴滚动,点B恰好经过原点.设顶点P(x,y)的轨迹方程是y=f(x),则对函数y=f(x)有下列判断:
如图放置的边长为1的正方形PABC沿x轴滚动,点B恰好经过原点.设顶点P(x,y)的轨迹方程是y=f(x),则对函数y=f(x)有下列判断: