题目内容
设函数
，则f（x）是
- A.最小正周期为π的奇函数
- B.最小正周期为π的偶函数
- C.最小正周期为2π的奇函数
- D.最小正周期为2π的偶函数
B
分析：利用两角和差的三角公式化简函数的解析式得f（x）=-cos2x+1，由 T=
求得周期，并判断奇偶性．
解答：函数=2（sinx•cos
-cosx•sin）•（coscosx-sinsinx）+1
=-2（
）+1=-cos2x+1，周期为 T==π，故为偶函数．
故选 B．
点评：本题考查两角和差的三角公式的应用，求函数的周期的方法，化简函数的解析式是解题的难点．
分析：利用两角和差的三角公式化简函数的解析式得f（x）=-cos2x+1，由 T=
求得周期，并判断奇偶性．解答：函数
=2（sinx•cos-cosx•sin）•（coscosx-sinsinx）+1 =-2（
）+1=-cos2x+1，周期为 T==π，故为偶函数．故选 B．
点评：本题考查两角和差的三角公式的应用，求函数的周期的方法，化简函数的解析式是解题的难点．
练习册系列答案
名校课堂系列答案
相关题目
，则f（x）是（ ）
，则f（x）是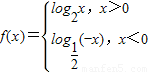
，则f（x）是 函数（填奇、偶、非奇非偶），若f（a）＞f（-a），则实数a的取值范围是 ．
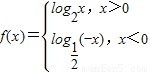，则f（x）是 函数（填奇、偶、非奇非偶），若f（a）＞f（-a），则实数a的取值范围是 ．