题目内容
设函数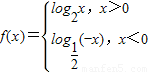 ,则f(x)是 函数(填奇、偶、非奇非偶),若f(a)>f(-a),则实数a的取值范围是 .
,则f(x)是 函数(填奇、偶、非奇非偶),若f(a)>f(-a),则实数a的取值范围是 .
【答案】分析:利用函数奇偶性的定义,可判断函数的奇偶性,确定函数的单调性,可求不等式.
解答:解:设x>0,则-x<0,∴f(-x)= =-log2x=-f(x);
=-log2x=-f(x);
设x<0,则-x>0,∴f(-x)=log2(-x)=- =-f(x)
=-f(x)
∴f(x)是奇函数;
∵f(a)>f(-a),∴f(a)>0,
∵函数 在(-∞,0),(0,+∞)上分别为增函数
在(-∞,0),(0,+∞)上分别为增函数
∴ 或
或
∴a>1或-1<a<0
故答案为:奇、(-1,0)∪(1,+∞).
点评:本题考查函数单调性与奇偶性的结合,考查学生的计算能力,属于基础题.
解答:解:设x>0,则-x<0,∴f(-x)=
 =-log2x=-f(x);
=-log2x=-f(x);设x<0,则-x>0,∴f(-x)=log2(-x)=-
 =-f(x)
=-f(x)∴f(x)是奇函数;
∵f(a)>f(-a),∴f(a)>0,
∵函数
 在(-∞,0),(0,+∞)上分别为增函数
在(-∞,0),(0,+∞)上分别为增函数∴
 或
或
∴a>1或-1<a<0
故答案为:奇、(-1,0)∪(1,+∞).
点评:本题考查函数单调性与奇偶性的结合,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
 ,则f(x)是
,则f(x)是 ,则f(x)是( )
,则f(x)是( ) ,则f(x)是
,则f(x)是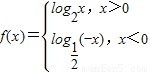 ,则f(x)是 函数(填奇、偶、非奇非偶),若f(a)>f(-a),则实数a的取值范围是 .
,则f(x)是 函数(填奇、偶、非奇非偶),若f(a)>f(-a),则实数a的取值范围是 .