题目内容
已知关于x的不等式x2-3x+m＜0的解集是{x|1＜x＜n}．
（1）求实数m，n的值；
（2）若正数a，b满足：ma+2nb=3，求a•b的最大值．
解：（1）由题意可知：1，n是x2-3x+m=0的两根，
所以
，解得：m=2，n=2；
（2）把m=2，n=2代入ma+2nb=3得
因为
，所以
，
得
，当且仅当
，即
时等号成立，
所以a•b的最大值为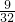
．
分析：（1）先根据题意可知：1，n是x2-3x+m=0的两根，然后利用根与系数的关系建立方程组，解之即可；
（2）将m与n的值代入，然后利用均值不等式即可求出a•b的最大值．
点评：本题主要考查了一元二次不等式的应用，以及根与系数的关系等有关知识，同时考查了计算能力，属于基础题．
所以
，解得：m=2，n=2；（2）把m=2，n=2代入ma+2nb=3得
因为
，所以，得
，当且仅当，即时等号成立，所以a•b的最大值为
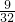．分析：（1）先根据题意可知：1，n是x2-3x+m=0的两根，然后利用根与系数的关系建立方程组，解之即可；
（2）将m与n的值代入，然后利用均值不等式即可求出a•b的最大值．
点评：本题主要考查了一元二次不等式的应用，以及根与系数的关系等有关知识，同时考查了计算能力，属于基础题．
练习册系列答案
相关题目
（1）几何证明选讲：如图，CB是⊙O的直径，AP是⊙O的切线，A为切点，AP与CB的延长线交于点P，若PA=8，PB=4，求AC的长度．