题目内容
把tan1,tan2,tan3,tan4按照由小到大的顺序排列,并说明理由.
活动:教师引导学生利用函数y=tanx的单调性探究解题方法.也可利用单位圆中的正切线探究解题方法.但要提醒学生注意本节中活动的结论:正切函数在定义域内的每个区间上都是增函数,但我们不可以说正切函数在整个定义域内是增函数.学生可能的错解有:
错解1:∵函数y=tanx是增函数,又1＜2＜3＜4,∴tan1＜tan2＜tan3＜tan4.
错解2:∵2和3的终边在第二象限,∴tan2,tan3都是负数.∵1和4的终边分别在第一和第三象限,∴tan1,tan4都是正数.
又∵函数y=tanx是增函数,且2＜3,1＜4,∴tan2＜tan3＜tan1＜tan4.
教师可放手让学生自己探究问题的解法.发现错解后不要直接纠正,立即给出正确解法,可再让学生讨论分析找出错的原因.
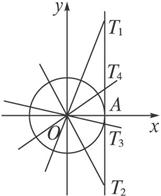
图6
解法一:∵函数y=tanx在区间(
,
)上是单调递增函数,
且tan1=tan(π+1),又
＜2＜3＜4＜π+1＜
,
∴tan2＜tan3＜tan4＜tan1.
解法二:如图6,1,2,3,4的正切函数线分别是AT1,AT2,AT3,AT4,
∴tan2＜tan3＜tan4＜tan1.
点评:本例重在让学生澄清正切函数单调性问题,这属于学生易错点.把正切函数y=tanx的单调性简单地说成“在定义域内是增函数”是不对的.
练习册系列答案
相关题目