题目内容
试把tan1、tan2、tan3、tan4按照从小到大的顺序排列,并说明理由.
解法一:∵函数y=tanx在区间[![]() ,
,![]() ]内是增函数且tan1=tan(π+1),
]内是增函数且tan1=tan(π+1),
又![]() <2<3<4<π+1<
<2<3<4<π+1<![]() ,
,
∴tan2<tan3<tan4<tan1.
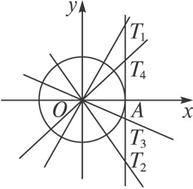
解法二:如图所示,1,2,3,4的正切函数线分别是AT1,AT2,AT3,AT4.所以tan2<tan3<tan4<tan1.
温馨提示
(1)将自变量化到同一单调区间,再利用单调性比较大小是比较三角函数值大小的重要方法.
(2)本题易产生以下两种误解:
误解一:∵函数y=tanx是增函数,又1<2<3<4,∴tan1<tan2<tan3<tan4.
误解二:∵2和3终边在第二象限,
∴tan2,tan3都是负数.
又∵1和4的终边分别在第一和第三象限,
∴tan1,tan4都是正数.
根据y=tanx是增函数且2<3,1<4,
∴tan2<tan3<tan1<tan4.
上述两个误解的根源在于混淆了函数单调性的概念.两个误解都把y=tanx视作定义域
上的单调增函数,从而导致了错误的结果.

练习册系列答案
相关题目
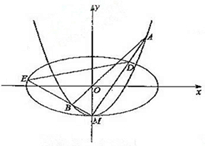 已知椭圆C1:
已知椭圆C1: