题目内容
【题目】如图,O为坐标原点,椭圆C1: ![]() +
+ ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 离心率为e1;双曲线C2:
=1(a>b>0)的左、右焦点分别为F1 , F2 , 离心率为e1;双曲线C2: ![]() ﹣
﹣ ![]() =1的左、右焦点分别为F3 , F4 , 离心率为e2 , 已知e1e2=
=1的左、右焦点分别为F3 , F4 , 离心率为e2 , 已知e1e2= ![]() ,且|F2F4|=
,且|F2F4|= ![]() ﹣1.
﹣1. 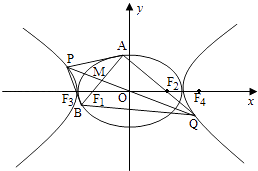
(1)求C1、C2的方程;
(2)过F1作C1的不垂直于y轴的弦AB,M为AB的中点,当直线OM与C2交于P,Q两点时,求四边形APBQ面积的最小值.
【答案】
(1)解:由题意可知, ![]() ,且
,且 ![]() .
.
∵e1e2= ![]() ,且|F2F4|=
,且|F2F4|= ![]() ﹣1.
﹣1.
∴ ![]() ,且
,且 ![]() .
.
解得: ![]() .
.
∴椭圆C1的方程为 ![]() ,双曲线C2的方程为
,双曲线C2的方程为 ![]() ;
;
(2)解:由(1)可得F1(﹣1,0).
∵直线AB不垂直于y轴,
∴设AB的方程为x=ny﹣1,
联立  ,得(n2+2)y2﹣2ny﹣1=0.
,得(n2+2)y2﹣2ny﹣1=0.
设A(x1,y1),B(x2,y2),M(x0,y0),
则 ![]() ,
, ![]() .
.
则 ![]()
= ![]() =
= ![]() .
.
∵M在直线AB上,
∴ ![]() .
.
直线PQ的方程为 ![]() ,
,
联立  ,得
,得 ![]() .
.
解得 ![]() ,代入
,代入 ![]() 得
得 ![]() .
.
由2﹣n2>0,得﹣ ![]() <n<
<n< ![]() .
.
∴P,Q的坐标分别为 ![]() ,
,
则P,Q到AB的距离分别为:  ,
,  .
.
∵P,Q在直线A,B的两端,
∴  .
.
则四边形APBQ的面积S= ![]() |AB|
|AB| ![]() .
.
∴当n2=0,即n=0时,四边形APBQ面积取得最小值2.
【解析】(1)由斜率公式写出e1 , e2 , 把双曲线的焦点用含有a,b的代数式表示,结合已知条件列关于a,b的方程组求解a,b的值,则圆锥曲线方程可求;(2)设出AB所在直线方程,和椭圆方程联立后得到关于y的一元二次方程,由根与系数的关系得到AB中点M的坐标,并由椭圆的焦点弦公式求出AB的长度,写出PQ的方程,和双曲线联立后解出P,Q的坐标,由点到直线的距离公式分别求出P,Q到AB的距离,然后代入代入三角形面积公式得四边形APBQ的面积,再由关于n的函数的单调性求得最值.

【题目】某零售店近5个月的销售额和利润额资料如下表:
商店名称 |
|
|
|
|
|
销售额 | 3 | 5 | 6 | 7 | 9 |
利润额 | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关关系;
(2)用最小二乘法计算利润额![]() 关于销售额
关于销售额![]() 的回归直线方程;
的回归直线方程;
(3)当销售额为4千万元时,利用(2)的结论估计该零售店的利润额(百万元).
[参考公式: ,
,![]() ]
]
