题目内容
(1)已知函数 ,求函数在区间[-2π,2π]上的单调增区间;
,求函数在区间[-2π,2π]上的单调增区间;
(2)计算: .
.
解:(1)由 (k∈Z)得
(k∈Z)得 (k∈Z),
(k∈Z),
当k=0时,得 ,
, ,且仅当k=0时符合题意,
,且仅当k=0时符合题意,
∴函数 在区间[-2π,2π]上的单调增区间是
在区间[-2π,2π]上的单调增区间是 .
.
(2) =
= =
= .
.
分析:(1)把“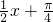 ”看成一个整体,利用正弦函数的增区间求出此函数的增区间,利用k的取值求出;
”看成一个整体,利用正弦函数的增区间求出此函数的增区间,利用k的取值求出;
(2)利用“切化弦”的基本思路,再结合三角恒等变换的公式将式子进行化简求值.
点评:本题考查了三角恒等变换的公式和正弦函数单调性性质的应用,主要利用对应的公式对解析式化简后,利用“整体思想”求函数的增区间,利用“切化弦”的基本思想进行化简求值,要求熟练掌握公式并能灵活运用.
 (k∈Z)得
(k∈Z)得 (k∈Z),
(k∈Z),当k=0时,得
 ,
, ,且仅当k=0时符合题意,
,且仅当k=0时符合题意,∴函数
 在区间[-2π,2π]上的单调增区间是
在区间[-2π,2π]上的单调增区间是 .
.(2)
 =
= =
= .
.分析:(1)把“
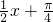 ”看成一个整体,利用正弦函数的增区间求出此函数的增区间,利用k的取值求出;
”看成一个整体,利用正弦函数的增区间求出此函数的增区间,利用k的取值求出;(2)利用“切化弦”的基本思路,再结合三角恒等变换的公式将式子进行化简求值.
点评:本题考查了三角恒等变换的公式和正弦函数单调性性质的应用,主要利用对应的公式对解析式化简后,利用“整体思想”求函数的增区间,利用“切化弦”的基本思想进行化简求值,要求熟练掌握公式并能灵活运用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 ,则
,则 …
… …+f(9)+f(10)=______.
…+f(9)+f(10)=______. 、…、
、…、 、
、 可一般表示为
可一般表示为 =
= 为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:
为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题: ,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值. ,则
,则 …
… …+f(9)+f(10)=______.
…+f(9)+f(10)=______. 、…、
、…、 、
、 可一般表示为
可一般表示为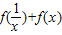 =
= 为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:
为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题: ,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.