题目内容
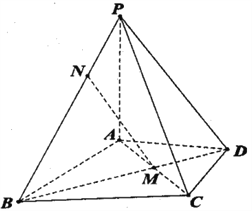
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 与
与![]() 的交点,点
的交点,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)由题意得![]() 是等边三角形,故得
是等边三角形,故得![]() ,于是
,于是![]() ,从而得
,从而得![]() ,所以
,所以![]() ,然后根据线面平行的判定定理可得结论成立.(2)由
,然后根据线面平行的判定定理可得结论成立.(2)由![]() 平面
平面![]() 可得
可得![]() ,于是
,于是![]() 平面
平面![]() .又
.又![]() ,所以直线
,所以直线![]() 与平面
与平面![]() 所成角即直线
所成角即直线![]() 与平面
与平面![]() 所成角,从而得到
所成角,从而得到![]() 即为所求角,然后根据解三角形可得所求.
即为所求角,然后根据解三角形可得所求.
详解:(1)因为![]() ,
,
所以![]() 垂直平分线段
垂直平分线段![]() .
.
又![]() ,
,
所以![]() .
.
在![]() 中,由余弦定理得
中,由余弦定理得
![]() ,
,
所以![]() .
.
又![]() ,
,
所以![]() 是等边三角形,
是等边三角形,
所以![]() ,
,
所以![]() ,
,
又因为![]() ,
,
所以![]() ,
,
所以![]() .
.
又![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,
,
又![]() ,
,
所以![]() 平面
平面![]() .
.
由(1)知![]() ,
,
所以直线![]() 与平面
与平面![]() 所成角即直线
所成角即直线![]() 与平面
与平面![]() 所成角,
所成角,
故![]() 即为所求的角.
即为所求的角.
在![]() 中,
中,![]() ,
,
所以![]() ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案【题目】某公司共有职工1500人,其中男职工1050人,女职工450人.为调查该公司职工每周平均上网的时间,采用分层抽样的方法,收集了300名职工每周平均上网时间的样本数据(单位:小时)

男职工 | 女职工 | 总计 | |
每周平均上网时间不超过4个小时 | |||
每周平均上网时间超过4个小时 | 70 | ||
总计 | 300 |
(Ⅰ)应收集多少名女职工样本数据?
(Ⅱ)根据这300个样本数据,得到职工每周平均上网时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .试估计该公司职工每周平均上网时间超过4小时的概率是多少?
.试估计该公司职工每周平均上网时间超过4小时的概率是多少?
(Ⅲ)在样本数据中,有70名女职工的每周平均上网时间超过4个小时.请将每周平均上网时间与性别的![]() 列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”
列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”
【题目】为了研究某种细菌随时间x变化,繁殖的个数,收集数据如下:
![]()
(1)用天数作解释变量,繁殖个数作预报变量,作出这些数据的散点图,根据散点图判断:![]() 与y=
与y=![]() 哪一个作为繁殖的个数y关于时间x变化的回归方程类型为最佳?(给出判断即可,不必说明理由)
哪一个作为繁殖的个数y关于时间x变化的回归方程类型为最佳?(给出判断即可,不必说明理由)
|
|
|
|
|
|
3.5 | 62.83 | 3.53 | 17.5 | 596.505 | 12.04 |
其中![]() ;
;![]()
(2)根据(1)的判断最佳结果及表中的数据,建立y关于x 的回归方程。
参考公式: 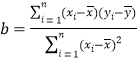
![]()